Introduction
Support Vector Machine (SVM) is a powerful algorithm to perform linear or nonlinear classification, regression or outlier detection. It is highly preferred since less computation power is required to produce reliable accuracy. SVM is one of the tools that should be applied for any Machine Learning project.
SVM Linear Classification¶
The Figure below shows the fundamental idea for SVM. We have two classes, circle (Class 1) and star (Class 2) based on two features (Feature 1 and Feature 2). The classes are linearly separable. Left Figure shows decision boundaries of three possible linear classifier: the decision boundaries of blue and red lines seems ok but decision boundary of dashed green line is very bad that cannot properly separate two classes. Although blue and red lines works perfectly for training set, they may be inefficient to predict a new instance. On the contrary, the decision boundary of solid black line in right Figure is achieved by SVM classifier; this line not only divides perfectly the two classes but also stays as far away from the closest training instances as possible. A SVM classifier works like fitting the widest possible street (parallel dashed lines) between the classes. This approach is called large margin classification.
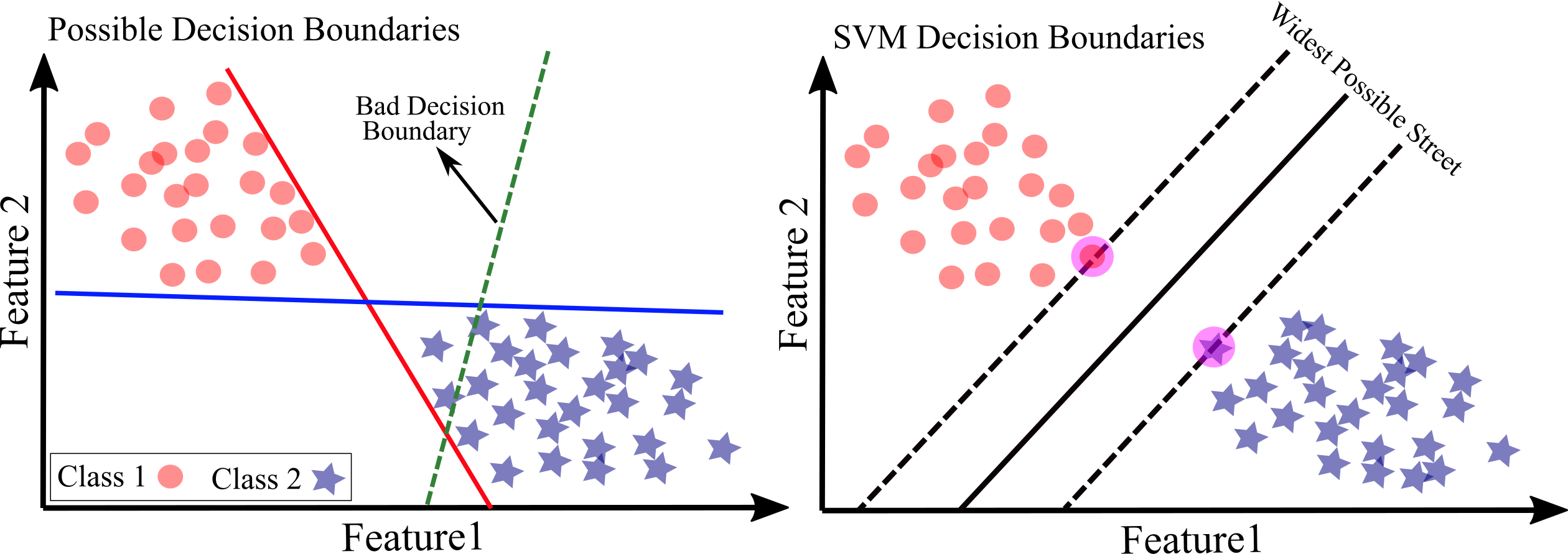
If you have more training instances that are “off the street”, the decision boundary will not be affected at all: the instances located on the edge of the street determine the decision boundaries. These instances shown in large circles are called the support vectors.
It must be noted that SVM are sensitive to the feature scales. It is highly recommended to standardize your features before applying SVM.
We just applied hard margin classification; however, in practice, it may not always works because 1- the data should be linearly separable that may not be the case all the time 2- SVM is very sensitive to outliers. To avoid this, we should have a more flexible SVM model that allows a few instances on the street and wrong sides. In fact, we should have a balance of large street and reduced margin violation. This technique is called soft margin classification.
We can control this balance using the C hyperparameter in Scikit-Learn’s SVM classes: by decreasing C value, we will have wider street but margin violations will also increase.
Figure below shows two classes (circle and star) that are non-linear. The decision boundaries and margins of for two soft margin SVM classifiers are shown in the Figure using different C hyperparameters. On the left Figure, C is low C=1, that means the margin is quite large, but we have many street violations. On the right Figure, by using a high C value, smaller margin is achieved leading to fewer margin violations. However, the left model is more likely better generalized since most margin violations are in correct side of the decision boundary. You can apply C as a regularization to reduce overfitting: reducing C leads to reduce overfitting and increasing C may lead to overfitting.

Lets apply a linear SVM model using Scikit-Learn for binary classification of Energy Efficiency Data Set used in previous lectures.
import pandas as pd
import numpy as np
df = pd.read_csv("Building_Heating_Load.csv") # Energy Efficiency Data Set
df[0:5]
| Relative Compactness | Surface Area | Wall Area | Roof Area | Overall Height | Orientation | Glazing Area | Glazing Area Distribution | Heating Load | Binary Classes | Multi-Classes | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.98 | 514.5 | 294.0 | 110.25 | 7.0 | 2 | 0.0 | 0 | 15.55 | Low Level | Level 2 |
| 1 | 0.98 | 514.5 | 294.0 | 110.25 | 7.0 | 3 | 0.0 | 0 | 15.55 | Low Level | Level 2 |
| 2 | 0.98 | 514.5 | 294.0 | 110.25 | 7.0 | 4 | 0.0 | 0 | 15.55 | Low Level | Level 2 |
| 3 | 0.98 | 514.5 | 294.0 | 110.25 | 7.0 | 5 | 0.0 | 0 | 15.55 | Low Level | Level 2 |
| 4 | 0.90 | 563.5 | 318.5 | 122.50 | 7.0 | 2 | 0.0 | 0 | 20.84 | Low Level | Level 2 |
df_binary=df.copy()
df_binary.drop(['Heating Load','Multi-Classes'], axis=1, inplace=True)
# Convert Class to Numbers
df_binary['Binary Classes']=df_binary['Binary Classes'].replace('Low Level', 0)
df_binary['Binary Classes']=df_binary['Binary Classes'].replace('High Level', 1)
df_binary[0:5]
| Relative Compactness | Surface Area | Wall Area | Roof Area | Overall Height | Orientation | Glazing Area | Glazing Area Distribution | Binary Classes | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.98 | 514.5 | 294.0 | 110.25 | 7.0 | 2 | 0.0 | 0 | 0 |
| 1 | 0.98 | 514.5 | 294.0 | 110.25 | 7.0 | 3 | 0.0 | 0 | 0 |
| 2 | 0.98 | 514.5 | 294.0 | 110.25 | 7.0 | 4 | 0.0 | 0 | 0 |
| 3 | 0.98 | 514.5 | 294.0 | 110.25 | 7.0 | 5 | 0.0 | 0 | 0 |
| 4 | 0.90 | 563.5 | 318.5 | 122.50 | 7.0 | 2 | 0.0 | 0 | 0 |
np.random.seed(32)
df_binary=df_binary.reindex(np.random.permutation(df_binary.index))
df_binary.reset_index(inplace=True, drop=True)
from sklearn.model_selection import StratifiedShuffleSplit
# Training and Test
spt = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_idx, test_idx in spt.split(df_binary, df_binary['Binary Classes']):
train_set_strat = df_binary.loc[train_idx]
test_set_strat = df_binary.loc[test_idx]
# Note that drop() creates a copy and does not affect train_set_strat
X_train = train_set_strat.drop("Binary Classes", axis=1)
y_train = train_set_strat["Binary Classes"].values
from sklearn.preprocessing import StandardScaler
# Standardize features
scaler = StandardScaler()
X_train=X_train.copy()
X_train_Std=scaler.fit_transform(X_train)
For a Linear SVC, we can either use Scikit-Learn with a linear SVM model using the LinearSVC or use the SVC class, using SVC(kernel="linear", C=1), but SVC is very slower for large training sets. SVC is more efficient for small data set that are non linearly separable. Lets try LinearSVC first:
from sklearn.svm import LinearSVC
# SVM Classifier model
np.random.seed(32)
svm_clf = LinearSVC(C=1)
svm_clf.fit(X_train_Std, y_train)
LinearSVC(C=1)
#svm_clf.intercept_
svm_clf.predict(X_train_Std[0:10])
array([0, 1, 1, 0, 0, 1, 0, 1, 0, 0], dtype=int64)
y_train[0:10]
array([0, 1, 1, 0, 0, 0, 0, 1, 0, 0], dtype=int64)
from sklearn.model_selection import cross_val_score
Accuracies=cross_val_score(svm_clf,X_train_Std,y_train, cv=4, scoring="accuracy")
Accuracies
array([0.92207792, 0.84415584, 0.90849673, 0.88888889])
from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(svm_clf,X_train_Std,y_train, cv=4)
from sklearn.metrics import confusion_matrix
def Conf_Matrix(predictor,x_train,y_train,perfect,sdt,axt=None):
'''Plot confusion matrix'''
ax1 = axt or plt.axes()
y_train_pred = cross_val_predict(predictor,x_train,y_train, cv=4)
if(perfect==1): y_train_pred=y_train
conf_mx=confusion_matrix(y_train, y_train_pred)
ii=0
if(len(conf_mx)<4):
im =ax1.matshow(conf_mx, cmap='jet', interpolation='nearest')
x=['Predicted\nNegative', 'Predicted\nPositive']; y=['Actual\nNegative', 'Actual\nPositive']
for (i, j), z in np.ndenumerate(conf_mx):
if(ii==0): al='TN= '
if(ii==1): al='FP= '
if(ii==2): al='FN= '
if(ii==3): al='TP= '
ax1.text(j, i, al+'{:0.0f}'.format(z), ha='center', va='center', fontweight='bold',fontsize=8.5)
ii=ii+1
ax1.set_xticks(np.arange(len(x)))
ax1.set_xticklabels(x,fontsize=6.5,y=0.97, rotation='horizontal')
ax1.set_yticks(np.arange(len(y)))
ax1.set_yticklabels(y,fontsize=6.5,x=0.035, rotation='horizontal')
else:
if(sdt==1):
row_sums = conf_mx.sum(axis=1, keepdims=True)
norm_confmx = conf_mx / row_sums
else:
norm_confmx=conf_mx
im =ax1.matshow(norm_confmx, cmap='jet', interpolation='nearest')
for (i, j), z in np.ndenumerate(norm_confmx):
if(sdt==1): ax1.text(j, i, '{:0.2f}'.format(z), ha='center', va='center', fontweight='bold')
else: ax1.text(j, i, '{:0.0f}'.format(z), ha='center', va='center', fontweight='bold')
cbar =plt.colorbar(im,shrink=0.3,orientation='vertical')
import matplotlib
import pylab as plt
font = {'size' : 6}
matplotlib.rc('font', **font)
fig = plt.subplots(figsize=(4.5, 4.5), dpi= 190, facecolor='w', edgecolor='k')
ax1=plt.subplot(1,2,1)
Conf_Matrix(svm_clf,X_train_Std,y_train,perfect=0,sdt=0,axt=ax1)
from sklearn.metrics import precision_score, recall_score
precision=precision_score(y_train, y_train_pred)
print('Precision= ',precision)
recall=recall_score(y_train, y_train_pred)
print('Recall (sensitivity)= ',recall)
Precision= 0.7545454545454545 Recall (sensitivity)= 0.6747967479674797
SVM Non-linear Classification¶
Apply Linear Regression¶
We applied linear SVM but some data may not be linearly separable. We saw in previous lectures that by adding new feature such as polynomial degree, nonlinear data can be converted to linear and then linear modeling can be applied. We can do the same for SVM. Lets apply a Linear SVM using polynomial features for a synthetic dataset.
font = {'size' : 12}
matplotlib.rc('font', **font)
fig = plt.subplots(figsize=(6.0, 4.5), dpi= 90, facecolor='w', edgecolor='k')
from sklearn.datasets import make_moons
x1, y1 = make_moons(n_samples=100, noise=0.2, random_state=22)
def moon_dataset(x1, y1, axes):
plt.plot(x1[:, 0][y1==0], x1[:, 1][y1==0], "bs",label='Class 0')
plt.plot(x1[:, 0][y1==1], x1[:, 1][y1==1], "r^",label='Class 1')
plt.xlabel(r"$X$", fontsize=18)
plt.ylabel(r"$Y$", fontsize=18, rotation=0)
plt.grid(True, which='both')
plt.legend(loc=4)
plt.axis(axes)
moon_dataset(x1, y1, [-1.5, 2.5, -1, 1.5])
plt.title('Synthetic Moon Dataset', fontsize=18)
plt.show()
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
polynomial_svm_clf = Pipeline([
("poly_features", PolynomialFeatures(degree=3)),
("scaler", StandardScaler()),
("svm_clf", LinearSVC(C=4, loss="hinge", random_state=70))
])
polynomial_svm_clf.fit(x1, y1)
Pipeline(steps=[('poly_features', PolynomialFeatures(degree=3)),
('scaler', StandardScaler()),
('svm_clf', LinearSVC(C=4, loss='hinge', random_state=70))])
Hinge Loss¶
Hinge loss is primarily used with SVM. It not only penalizes the wrong predictions but also not confident about right predictions. The function for the hinge loss is max(0, 1 – t); for t ≥ 1, it is equal to 0. If t < 1, the derivative of lost Hinge loss is equal to –1; otherwise, if t > 1, the derivative is 0. So, the Gradient Descent can be used to calculate optimum weights. The code below shows Hinge loss
font = {'size' : 12}
matplotlib.rc('font', **font)
fig = plt.subplots(figsize=(6.0, 3.5), dpi= 90, facecolor='w', edgecolor='k')
t = np.linspace(-5, 8, 200)
hing = np.where(1 - t < 0, 0, 1 - t) # max(0, 1-t)
plt.plot(t, hing, "r-", linewidth=4, label="$max(0, 1 - t)$")
plt.grid(True, which='both')
plt.axhline(y=0, color='k'); plt.axvline(x=0, color='k')
plt.xlabel("$t$", fontsize=16)
plt.title("Hing Loss Function", fontsize=18)
plt.axis([-4, 6, -1, 4])
plt.legend(loc=1, fontsize=16)
plt.show()
font = {'size' : 12}
matplotlib.rc('font', **font)
fig = plt.subplots(figsize=(6.0, 4.5), dpi= 80, facecolor='w', edgecolor='k')
def predictions(clf, ax):
x_0 = np.linspace(ax[0], ax[1], 100)
x_1 = np.linspace(ax[2], ax[3], 100)
x0, x1 = np.meshgrid(x_0, x_1)
X = np.c_[x0.ravel(), x1.ravel()]
y_pred = clf.predict(X).reshape(x0.shape)
y_decision = clf.decision_function(X).reshape(x0.shape)
plt.contourf(x0, x1, y_pred, cmap='jet', alpha=0.3)
plt.contourf(x0, x1, y_decision, cmap='jet', alpha=0.2)
predictions(polynomial_svm_clf, [-1.5, 2.5, -1, 1.5])
moon_dataset(x1, y1, [-1.5, 2.5, -1, 1.5])
plt.title('Prediction of Classes with Linear SVM \n classifier using polynomial features', fontsize=16)
plt.show()
Apply Polynomial Kernel¶
The problem is a low polynomial degree is not efficient for very complex datasets, and high polynomial degree can create a huge number of features which makes the model too slow. A mathematical technique called the kernel trick makes it possible to deal with complex datasets; you do not need to add any feature for this approach. Kernel trick is implemented by the SVC in Scikit-Learn. Lets apply polynomial Kernel for previous example:
from sklearn.svm import SVC
np.random.seed(32)
poly_kernel_svm_clf = Pipeline([("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=5, coef0=3, C=1))])
poly_kernel_svm_clf.fit(x1, y1)
Pipeline(steps=[('scaler', StandardScaler()),
('svm_clf', SVC(C=1, coef0=3, degree=5, kernel='poly'))])
font = {'size' : 12}
matplotlib.rc('font', **font)
fig = plt.subplots(figsize=(6.0, 4.5), dpi= 80, facecolor='w', edgecolor='k')
predictions(poly_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
moon_dataset(x1, y1, [-1.5, 2.5, -1, 1.5])
plt.title('Prediction of Classes with SVM polynomial kernel \n Degree=3, Coef0=2, C=1.5 ', fontsize=15)
plt.show()
By increasing C parameter, the model leads to overfit. See the code below for an overfitted model with C=200
font = {'size' : 12}
matplotlib.rc('font', **font)
fig = plt.subplots(figsize=(6.0, 4.5), dpi= 80, facecolor='w', edgecolor='k')
np.random.seed(32)
poly_kernel_svm_clf = Pipeline([("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=3, coef0=2, C=200))])
poly_kernel_svm_clf.fit(x1, y1)
predictions(poly_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
moon_dataset(x1, y1, [-1.5, 2.5, -1, 1.5])
plt.title('Prediction of Classes with SVM polynomial kernel \n Degree=3, Coef0=2, C=200 ', fontsize=15)
plt.show()
The figure below shows SVM polynomial kernel for different values for hyperparameters. The hyperparameter coef0 controls the model's influence by highdegree polynomials versus low-degree polynomials.
font = {'size' : 12}
matplotlib.rc('font', **font)
fig, axs = plt.subplots(figsize=(10, 8), dpi= 100, facecolor='w', edgecolor='k')
fig.subplots_adjust(hspace = 0.35, wspace=0.2)
ax1=plt.subplot(2,2,1)
np.random.seed(32)
poly_kernel_svm_clf = Pipeline([("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=3, coef0=2, C=1.5))])
poly_kernel_svm_clf.fit(x1, y1)
predictions(poly_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
moon_dataset(x1, y1, [-1.5, 2.5, -1, 1.5])
plt.title('Degree=3, Coef0=2, C=1.5 ', fontsize=12)
ax2=plt.subplot(2,2,2)
np.random.seed(32)
poly_kernel_svm_clf = Pipeline([("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=10, coef0=4, C=15))])
poly_kernel_svm_clf.fit(x1, y1)
predictions(poly_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
moon_dataset(x1, y1, [-1.5, 2.5, -1, 1.5])
plt.title('Degree=10, Coef0=4, C=15 ', fontsize=12)
ax3=plt.subplot(2,2,3)
np.random.seed(32)
poly_kernel_svm_clf = Pipeline([("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=12, coef0=20, C=3))])
poly_kernel_svm_clf.fit(x1, y1)
predictions(poly_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
moon_dataset(x1, y1, [-1.5, 2.5, -1, 1.5])
plt.title('Degree=12, Coef0=20, C=3 ', fontsize=12)
ax4=plt.subplot(2,2,4)
np.random.seed(32)
poly_kernel_svm_clf = Pipeline([("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=20, coef0=1, C=15))])
poly_kernel_svm_clf.fit(x1, y1)
predictions(poly_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
moon_dataset(x1, y1, [-1.5, 2.5, -1, 1.5])
plt.title('Degree=20, Coef0=1, C=15 ', fontsize=12)
plt.show()
The question is how we can find optimum hyper parameters? We will shows how to use Scikit-learn Grid Search to find the best values.
Apply Gaussian RBF Kernel¶
Another technique to solve nonlinear problem is to add features from similarity function. It works based on measuring how much each instance is similar to a particular landmark. The function that measures similarity is the Gaussian Radial Basis Function (RBF) (Aurélien Géron, 2019).
The following code shows how to apply the Gaussian RBF kernel using the SVC class:
np.random.seed(32)
rbf_kernel_svm_clf = Pipeline([("scaler", StandardScaler()), ("svm_clf", SVC(kernel="rbf", gamma=7, C=0.01))])
rbf_kernel_svm_clf.fit(x1, y1)
Pipeline(steps=[('scaler', StandardScaler()),
('svm_clf', SVC(C=0.01, gamma=7))])
This model is represented on the top left of Figure below. There are 3 other Figures trained with different values of hyperparameters C and gamma ($\gamma$). If we decrease $\gamma$, the bell-shape curve gets wider, and smaller $\gamma$ makes the bell-shape curve narrower. So, we can use $\gamma$ as regularization hyperparameter: reducing $\gamma$ leads to avoid overfitting and; however, if your model is underfitting, you should increase $\gamma$ (Similar to C).
font = {'size' : 12}
matplotlib.rc('font', **font)
fig, axs = plt.subplots(figsize=(10, 8), dpi= 100, facecolor='w', edgecolor='k')
fig.subplots_adjust(hspace = 0.35, wspace=0.2)
ax1=plt.subplot(2,2,1)
predictions(rbf_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
moon_dataset(x1, y1, [-1.5, 2.5, -1, 1.5])
plt.title(r'$\gamma=7$'+', C=0.01 ', fontsize=12)
ax2=plt.subplot(2,2,2)
np.random.seed(32)
rbf_kernel_svm_clf = Pipeline([("scaler", StandardScaler()), ("svm_clf", SVC(kernel="rbf", gamma=7, C=800))])
rbf_kernel_svm_clf.fit(x1, y1)
predictions(rbf_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
moon_dataset(x1, y1, [-1.5, 2.5, -1, 1.5])
plt.title(r'$\gamma=7$'+', C=800 ', fontsize=12)
ax3=plt.subplot(2,2,3)
np.random.seed(32)
rbf_kernel_svm_clf = Pipeline([("scaler", StandardScaler()), ("svm_clf", SVC(kernel="rbf", gamma=0.2, C=0.01))])
rbf_kernel_svm_clf.fit(x1, y1)
predictions(rbf_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
moon_dataset(x1, y1, [-1.5, 2.5, -1, 1.5])
plt.title(r'$\gamma=0.2$'+', C=0.01 ', fontsize=12)
ax4=plt.subplot(2,2,4)
np.random.seed(32)
rbf_kernel_svm_clf = Pipeline([("scaler", StandardScaler()), ("svm_clf", SVC(kernel="rbf", gamma=0.2, C=800))])
rbf_kernel_svm_clf.fit(x1, y1)
predictions(rbf_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
moon_dataset(x1, y1, [-1.5, 2.5, -1, 1.5])
plt.title(r'$\gamma=0.2$'+', C=800 ', fontsize=12)
plt.show()
There are several options to choose for classification with SVM but you should always try the linear kernel first because it is much faster especially for large training set. You can apply Gaussian RBF kernel if the training set is not too large. It is recommended to use cross-validation to make sure if computational cost is fine to run Gaussian RBF kernel.
Regression with SVM¶
As we discussed, the SVM algorithm is compatible with both regression and classification tasks although it is primarily applied for classification. Linear and non-linear regression can be applied for SVM by reversing the objective of classification: the largest possible street between two classes while limiting margin violations. The trick is to fit as many instances as possible on the street at the same time limiting margin violations (i.e., instances off the street). The width of the street can be controlled by $\epsilon$. The lower higher the $\epsilon$, the wider the street.
Linear Model¶
np.random.seed(32)
n = 100
X = 3 * np.random.rand(n, 1)
y = (3 - 4 * X + 2*np.random.randn(n, 1)).ravel()
from sklearn.svm import LinearSVR
reg_svm_1 = LinearSVR(epsilon=2, random_state=32)
reg_svm_2 = LinearSVR(epsilon=1, random_state=32)
reg_svm_1.fit(X, y)
reg_svm_2.fit(X, y)
LinearSVR(epsilon=1, random_state=32)
def support_vectors(X, y,svm_reg):
y_pred = svm_reg.predict(X)
off = (np.abs(y - y_pred) >= svm_reg.epsilon)
idx=np.argwhere(off)
return idx
idx_1_reg_svm = support_vectors(X, y, reg_svm_1)
idx_2_reg_svm = support_vectors(X, y, reg_svm_2)
def svm_regression_plot(svm_reg, X, y,idx,axes,loc):
x1 = np.linspace(axes[0], axes[1], 100).reshape(100, 1)
y_pred = svm_reg.predict(x1)
plt.plot(x1, y_pred, 'k-', linewidth=4, label='Fitted Model')
plt.plot(x1, y_pred + svm_reg.epsilon, 'r--', linewidth=2, label='Upper Street')
plt.plot(x1, y_pred - svm_reg.epsilon, 'g--', linewidth=2, label='Lower Street')
plt.scatter(X[idx], y[idx], s=160, facecolors='m')
plt.plot(X, y, 'bo')
plt.xlabel('X', fontsize=18)
plt.legend(loc=loc, fontsize=12)
plt.axis(axes)
font = {'size' : 12}
matplotlib.rc('font', **font)
fig, axs = plt.subplots(figsize=(11, 4), dpi= 95, facecolor='w', edgecolor='k')
plt.subplot(1,2,1)
svm_regression_plot(reg_svm_1, X, y,idx_1_reg_svm, [0, 3, -10, 4],loc=3)
plt.title('SVM Regression for '+r'$\epsilon =$'+str(reg_svm_1.epsilon), fontsize=16)
plt.ylabel('y', fontsize=18, rotation=0)
plt.subplot(1,2,2)
svm_regression_plot(reg_svm_2, X, y,idx_2_reg_svm, [0, 3, -10, 4],loc=3)
plt.title('SVM Regression for '+r'$\epsilon =$'+str(reg_svm_2.epsilon), fontsize=16)
plt.ylabel('y', fontsize=18, rotation=0)
plt.show()
Polynomial Model¶
np.random.seed(45)
n = 100
X = 2 * np.random.rand(n, 1) - 1
y = (0.8 + 0.4 * X - 2*X**2 + 0.5*np.random.randn(n, 1)).ravel()
from sklearn.svm import SVR
poly_svm_reg1 = SVR(kernel="poly", degree=2, C=80, epsilon=0.75, gamma="scale")
poly_svm_reg2 = SVR(kernel="poly", degree=2, C=5, epsilon=0.3, gamma="scale")
poly_svm_reg1.fit(X, y)
poly_svm_reg2.fit(X, y)
SVR(C=5, degree=2, epsilon=0.3, kernel='poly')
idx_1_reg_svm = support_vectors(X, y, poly_svm_reg1)
idx_2_reg_svm = support_vectors(X, y, poly_svm_reg2)
font = {'size' : 12}
matplotlib.rc('font', **font)
fig, axs = plt.subplots(figsize=(11, 4), dpi= 95, facecolor='w', edgecolor='k')
plt.subplot(1,2,1)
svm_regression_plot(poly_svm_reg1, X, y,idx_1_reg_svm, [-1, 1, -2, 3],loc=1)
plt.title('Degree=2, '+'C=75, '+ r'$\epsilon =$'+str(reg_svm_1.epsilon), fontsize=16)
plt.subplot(1,2,2)
svm_regression_plot(poly_svm_reg2, X, y,idx_2_reg_svm, [-1, 1, -2, 3],loc=1)
plt.title('Degree=2, '+'C=0.01, '+ r'$\epsilon =$'+str(reg_svm_2.epsilon), fontsize=16)
plt.ylabel('y', fontsize=18, rotation=0)
plt.show()
Fine-Tune Your Model¶
All ML algorithms have some hyperparameters. The question is how to an optimum value for each hyperparameter. For example, SVR has the hyperparameters kernel, degree, C, degree, epsilon... You should fine-tune these hyperparameters for optimum prediction. One way is to change the hyperparameters manually, until you achieve a reasonable combination of hyperparameter values. You may not have time to do this since exploring many combinations would be very tedious work. This can be automatically done by Scikit-Learn’ Grid Search and Randomized Search to fine tune these parameters:
Grid Search¶
Scikit-Learn’s GridSearchCV search parameters that maximize the performance. You need to define a list of some values for each parameter, GridSearchCV evaluates all the possible combinations of hyperparameters by using cross-validation. The following code searches for the best combination of hyperparameter values for the DecisionTreeClassifier:
from sklearn.model_selection import GridSearchCV
np.random.seed(42)
svm = SVR()
params = {'kernel': ['poly','linear'],
'degree': [1,2,4,5], 'C':[1,10,15,20,25], 'epsilon':[0.5,0.6,0.65,0.7,0.75,0.8]}
svm_search_cv = GridSearchCV(svm, params, cv=4,scoring="neg_mean_squared_error")
svm_search_cv.fit(X,y)
# Optimum values for the hyperparameters are:
svm_search_cv.best_params_
{'C': 1, 'degree': 2, 'epsilon': 0.7, 'kernel': 'poly'}
GridSearchCV search for $2 \times 4 \times 5 \times 7 =280$ combinations of 'kernel', 'degree', 'C' and epsilon' to find the best combination of these two parameters.
cvreslt=svm_search_cv.cv_results_
cvreslt_params=[str(i) for i in cvreslt["params"]]
for mean_score, params in sorted(zip(cvreslt["mean_test_score"], cvreslt_params)):
print(np.sqrt(-mean_score), params)
0.8605884691869644 {'C': 20, 'degree': 5, 'epsilon': 0.5, 'kernel': 'poly'}
0.8605558839854696 {'C': 1, 'degree': 5, 'epsilon': 0.5, 'kernel': 'poly'}
0.8605545648439008 {'C': 10, 'degree': 5, 'epsilon': 0.5, 'kernel': 'poly'}
0.8605538330309542 {'C': 15, 'degree': 5, 'epsilon': 0.5, 'kernel': 'poly'}
0.8605523714701415 {'C': 25, 'degree': 5, 'epsilon': 0.5, 'kernel': 'poly'}
0.8546116631483488 {'C': 1, 'degree': 5, 'epsilon': 0.7, 'kernel': 'poly'}
0.8546083472366983 {'C': 10, 'degree': 5, 'epsilon': 0.7, 'kernel': 'poly'}
0.8546046689890405 {'C': 20, 'degree': 5, 'epsilon': 0.7, 'kernel': 'poly'}
0.8546028322694731 {'C': 25, 'degree': 5, 'epsilon': 0.7, 'kernel': 'poly'}
0.8545858200093039 {'C': 15, 'degree': 5, 'epsilon': 0.7, 'kernel': 'poly'}
0.8540731032471469 {'C': 25, 'degree': 5, 'epsilon': 0.75, 'kernel': 'poly'}
0.8540711071516155 {'C': 20, 'degree': 5, 'epsilon': 0.75, 'kernel': 'poly'}
0.8540691112240945 {'C': 15, 'degree': 5, 'epsilon': 0.75, 'kernel': 'poly'}
0.8540671154834044 {'C': 10, 'degree': 5, 'epsilon': 0.75, 'kernel': 'poly'}
0.8540635235922722 {'C': 1, 'degree': 5, 'epsilon': 0.75, 'kernel': 'poly'}
0.8514874476105785 {'C': 15, 'degree': 1, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514874476105785 {'C': 15, 'degree': 2, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514874476105785 {'C': 15, 'degree': 4, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514874476105785 {'C': 15, 'degree': 5, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514808673922851 {'C': 20, 'degree': 1, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514808673922851 {'C': 20, 'degree': 2, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514808673922851 {'C': 20, 'degree': 4, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514808673922851 {'C': 20, 'degree': 5, 'epsilon': 0.8, 'kernel': 'linear'}
0.851448397583382 {'C': 10, 'degree': 1, 'epsilon': 0.8, 'kernel': 'poly'}
0.8514251428295198 {'C': 1, 'degree': 1, 'epsilon': 0.8, 'kernel': 'poly'}
0.8514085639409412 {'C': 25, 'degree': 1, 'epsilon': 0.8, 'kernel': 'poly'}
0.8514084726615727 {'C': 25, 'degree': 1, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514084726615727 {'C': 25, 'degree': 2, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514084726615727 {'C': 25, 'degree': 4, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514084726615727 {'C': 25, 'degree': 5, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514084473078057 {'C': 20, 'degree': 1, 'epsilon': 0.8, 'kernel': 'poly'}
0.8514083306657327 {'C': 15, 'degree': 1, 'epsilon': 0.8, 'kernel': 'poly'}
0.8514081775786265 {'C': 10, 'degree': 1, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514081775786265 {'C': 10, 'degree': 2, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514081775786265 {'C': 10, 'degree': 4, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514081775786265 {'C': 10, 'degree': 5, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514080005303009 {'C': 1, 'degree': 1, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514080005303009 {'C': 1, 'degree': 2, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514080005303009 {'C': 1, 'degree': 4, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514080005303009 {'C': 1, 'degree': 5, 'epsilon': 0.8, 'kernel': 'linear'}
0.8508607634564316 {'C': 1, 'degree': 5, 'epsilon': 0.6, 'kernel': 'poly'}
0.850858378190749 {'C': 10, 'degree': 5, 'epsilon': 0.6, 'kernel': 'poly'}
0.8508570555659717 {'C': 15, 'degree': 5, 'epsilon': 0.6, 'kernel': 'poly'}
0.850855735564398 {'C': 20, 'degree': 5, 'epsilon': 0.6, 'kernel': 'poly'}
0.8508544166169636 {'C': 25, 'degree': 5, 'epsilon': 0.6, 'kernel': 'poly'}
0.8508052620294099 {'C': 25, 'degree': 5, 'epsilon': 0.8, 'kernel': 'poly'}
0.8508021616390155 {'C': 20, 'degree': 5, 'epsilon': 0.8, 'kernel': 'poly'}
0.8507990612674942 {'C': 15, 'degree': 5, 'epsilon': 0.8, 'kernel': 'poly'}
0.850795961145672 {'C': 10, 'degree': 5, 'epsilon': 0.8, 'kernel': 'poly'}
0.8507903810737515 {'C': 1, 'degree': 5, 'epsilon': 0.8, 'kernel': 'poly'}
0.8471125824502213 {'C': 1, 'degree': 5, 'epsilon': 0.65, 'kernel': 'poly'}
0.8471122511117735 {'C': 10, 'degree': 5, 'epsilon': 0.65, 'kernel': 'poly'}
0.8471120688097363 {'C': 15, 'degree': 5, 'epsilon': 0.65, 'kernel': 'poly'}
0.8471118885361072 {'C': 20, 'degree': 5, 'epsilon': 0.65, 'kernel': 'poly'}
0.8471117093573483 {'C': 25, 'degree': 5, 'epsilon': 0.65, 'kernel': 'poly'}
0.8430268868601246 {'C': 25, 'degree': 1, 'epsilon': 0.75, 'kernel': 'poly'}
0.8430267577694824 {'C': 20, 'degree': 1, 'epsilon': 0.75, 'kernel': 'poly'}
0.8430266285442783 {'C': 15, 'degree': 1, 'epsilon': 0.75, 'kernel': 'poly'}
0.8430264994049629 {'C': 10, 'degree': 1, 'epsilon': 0.75, 'kernel': 'poly'}
0.8430264792067719 {'C': 25, 'degree': 1, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430264792067719 {'C': 25, 'degree': 2, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430264792067719 {'C': 25, 'degree': 4, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430264792067719 {'C': 25, 'degree': 5, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430264315566223 {'C': 20, 'degree': 1, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430264315566223 {'C': 20, 'degree': 2, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430264315566223 {'C': 20, 'degree': 4, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430264315566223 {'C': 20, 'degree': 5, 'epsilon': 0.75, 'kernel': 'linear'}
0.843026383904745 {'C': 15, 'degree': 1, 'epsilon': 0.75, 'kernel': 'linear'}
0.843026383904745 {'C': 15, 'degree': 2, 'epsilon': 0.75, 'kernel': 'linear'}
0.843026383904745 {'C': 15, 'degree': 4, 'epsilon': 0.75, 'kernel': 'linear'}
0.843026383904745 {'C': 15, 'degree': 5, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430263362454073 {'C': 10, 'degree': 1, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430263362454073 {'C': 10, 'degree': 2, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430263362454073 {'C': 10, 'degree': 4, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430263362454073 {'C': 10, 'degree': 5, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430262669762422 {'C': 1, 'degree': 1, 'epsilon': 0.75, 'kernel': 'poly'}
0.8430262504292136 {'C': 1, 'degree': 1, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430262504292136 {'C': 1, 'degree': 2, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430262504292136 {'C': 1, 'degree': 4, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430262504292136 {'C': 1, 'degree': 5, 'epsilon': 0.75, 'kernel': 'linear'}
0.8401670805663319 {'C': 25, 'degree': 1, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401670805663319 {'C': 25, 'degree': 2, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401670805663319 {'C': 25, 'degree': 4, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401670805663319 {'C': 25, 'degree': 5, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401670604564085 {'C': 20, 'degree': 1, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401670604564085 {'C': 20, 'degree': 2, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401670604564085 {'C': 20, 'degree': 4, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401670604564085 {'C': 20, 'degree': 5, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401670402708983 {'C': 15, 'degree': 1, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401670402708983 {'C': 15, 'degree': 2, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401670402708983 {'C': 15, 'degree': 4, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401670402708983 {'C': 15, 'degree': 5, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401670202885926 {'C': 10, 'degree': 1, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401670202885926 {'C': 10, 'degree': 2, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401670202885926 {'C': 10, 'degree': 4, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401670202885926 {'C': 10, 'degree': 5, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401669841075612 {'C': 1, 'degree': 1, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401669841075612 {'C': 1, 'degree': 2, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401669841075612 {'C': 1, 'degree': 4, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401669841075612 {'C': 1, 'degree': 5, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401669741160442 {'C': 1, 'degree': 1, 'epsilon': 0.65, 'kernel': 'poly'}
0.8401669205370896 {'C': 10, 'degree': 1, 'epsilon': 0.65, 'kernel': 'poly'}
0.8401668907279854 {'C': 15, 'degree': 1, 'epsilon': 0.65, 'kernel': 'poly'}
0.8401668610077485 {'C': 20, 'degree': 1, 'epsilon': 0.65, 'kernel': 'poly'}
0.8401668312198504 {'C': 25, 'degree': 1, 'epsilon': 0.65, 'kernel': 'poly'}
0.8399343310560787 {'C': 1, 'degree': 1, 'epsilon': 0.7, 'kernel': 'poly'}
0.8399331356855028 {'C': 20, 'degree': 1, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399331356855028 {'C': 20, 'degree': 2, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399331356855028 {'C': 20, 'degree': 4, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399331356855028 {'C': 20, 'degree': 5, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399331256587192 {'C': 15, 'degree': 1, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399331256587192 {'C': 15, 'degree': 2, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399331256587192 {'C': 15, 'degree': 4, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399331256587192 {'C': 15, 'degree': 5, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399331156316959 {'C': 10, 'degree': 1, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399331156316959 {'C': 10, 'degree': 2, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399331156316959 {'C': 10, 'degree': 4, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399331156316959 {'C': 10, 'degree': 5, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399330975897537 {'C': 1, 'degree': 1, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399330975897537 {'C': 1, 'degree': 2, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399330975897537 {'C': 1, 'degree': 4, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399330975897537 {'C': 1, 'degree': 5, 'epsilon': 0.7, 'kernel': 'linear'}
0.839932903741658 {'C': 15, 'degree': 1, 'epsilon': 0.7, 'kernel': 'poly'}
0.8399328397701434 {'C': 20, 'degree': 1, 'epsilon': 0.7, 'kernel': 'poly'}
0.8399327758367391 {'C': 25, 'degree': 1, 'epsilon': 0.7, 'kernel': 'poly'}
0.8399313501449663 {'C': 25, 'degree': 1, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399313501449663 {'C': 25, 'degree': 2, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399313501449663 {'C': 25, 'degree': 4, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399313501449663 {'C': 25, 'degree': 5, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399229686666608 {'C': 10, 'degree': 1, 'epsilon': 0.7, 'kernel': 'poly'}
0.834721474921055 {'C': 15, 'degree': 1, 'epsilon': 0.6, 'kernel': 'linear'}
0.834721474921055 {'C': 15, 'degree': 2, 'epsilon': 0.6, 'kernel': 'linear'}
0.834721474921055 {'C': 15, 'degree': 4, 'epsilon': 0.6, 'kernel': 'linear'}
0.834721474921055 {'C': 15, 'degree': 5, 'epsilon': 0.6, 'kernel': 'linear'}
0.834668370471576 {'C': 1, 'degree': 1, 'epsilon': 0.6, 'kernel': 'poly'}
0.8346325886910254 {'C': 10, 'degree': 1, 'epsilon': 0.6, 'kernel': 'poly'}
0.8345884343506251 {'C': 15, 'degree': 1, 'epsilon': 0.6, 'kernel': 'poly'}
0.8345805968009083 {'C': 25, 'degree': 1, 'epsilon': 0.6, 'kernel': 'poly'}
0.8345801920617625 {'C': 20, 'degree': 1, 'epsilon': 0.6, 'kernel': 'poly'}
0.8345788431461214 {'C': 25, 'degree': 1, 'epsilon': 0.6, 'kernel': 'linear'}
0.8345788431461214 {'C': 25, 'degree': 2, 'epsilon': 0.6, 'kernel': 'linear'}
0.8345788431461214 {'C': 25, 'degree': 4, 'epsilon': 0.6, 'kernel': 'linear'}
0.8345788431461214 {'C': 25, 'degree': 5, 'epsilon': 0.6, 'kernel': 'linear'}
0.8345787892877505 {'C': 20, 'degree': 1, 'epsilon': 0.6, 'kernel': 'linear'}
0.8345787892877505 {'C': 20, 'degree': 2, 'epsilon': 0.6, 'kernel': 'linear'}
0.8345787892877505 {'C': 20, 'degree': 4, 'epsilon': 0.6, 'kernel': 'linear'}
0.8345787892877505 {'C': 20, 'degree': 5, 'epsilon': 0.6, 'kernel': 'linear'}
0.8345786815836475 {'C': 10, 'degree': 1, 'epsilon': 0.6, 'kernel': 'linear'}
0.8345786815836475 {'C': 10, 'degree': 2, 'epsilon': 0.6, 'kernel': 'linear'}
0.8345786815836475 {'C': 10, 'degree': 4, 'epsilon': 0.6, 'kernel': 'linear'}
0.8345786815836475 {'C': 10, 'degree': 5, 'epsilon': 0.6, 'kernel': 'linear'}
0.8345785846382784 {'C': 1, 'degree': 1, 'epsilon': 0.6, 'kernel': 'linear'}
0.8345785846382784 {'C': 1, 'degree': 2, 'epsilon': 0.6, 'kernel': 'linear'}
0.8345785846382784 {'C': 1, 'degree': 4, 'epsilon': 0.6, 'kernel': 'linear'}
0.8345785846382784 {'C': 1, 'degree': 5, 'epsilon': 0.6, 'kernel': 'linear'}
0.8333730733642384 {'C': 25, 'degree': 1, 'epsilon': 0.5, 'kernel': 'poly'}
0.8333729986052557 {'C': 15, 'degree': 1, 'epsilon': 0.5, 'kernel': 'poly'}
0.8333729612676628 {'C': 10, 'degree': 1, 'epsilon': 0.5, 'kernel': 'poly'}
0.8333728940103742 {'C': 1, 'degree': 1, 'epsilon': 0.5, 'kernel': 'poly'}
0.833372742677603 {'C': 10, 'degree': 1, 'epsilon': 0.5, 'kernel': 'linear'}
0.833372742677603 {'C': 10, 'degree': 2, 'epsilon': 0.5, 'kernel': 'linear'}
0.833372742677603 {'C': 10, 'degree': 4, 'epsilon': 0.5, 'kernel': 'linear'}
0.833372742677603 {'C': 10, 'degree': 5, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333726706233276 {'C': 15, 'degree': 1, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333726706233276 {'C': 15, 'degree': 2, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333726706233276 {'C': 15, 'degree': 4, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333726706233276 {'C': 15, 'degree': 5, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333725264540203 {'C': 25, 'degree': 1, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333725264540203 {'C': 25, 'degree': 2, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333725264540203 {'C': 25, 'degree': 4, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333725264540203 {'C': 25, 'degree': 5, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333639152841654 {'C': 20, 'degree': 1, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333639152841654 {'C': 20, 'degree': 2, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333639152841654 {'C': 20, 'degree': 4, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333639152841654 {'C': 20, 'degree': 5, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333606544199835 {'C': 20, 'degree': 1, 'epsilon': 0.5, 'kernel': 'poly'}
0.8318277355123119 {'C': 1, 'degree': 1, 'epsilon': 0.5, 'kernel': 'linear'}
0.8318277355123119 {'C': 1, 'degree': 2, 'epsilon': 0.5, 'kernel': 'linear'}
0.8318277355123119 {'C': 1, 'degree': 4, 'epsilon': 0.5, 'kernel': 'linear'}
0.8318277355123119 {'C': 1, 'degree': 5, 'epsilon': 0.5, 'kernel': 'linear'}
0.6043793416042527 {'C': 20, 'degree': 4, 'epsilon': 0.8, 'kernel': 'poly'}
0.604378696369846 {'C': 15, 'degree': 4, 'epsilon': 0.8, 'kernel': 'poly'}
0.6043780514193523 {'C': 10, 'degree': 4, 'epsilon': 0.8, 'kernel': 'poly'}
0.6043768904899779 {'C': 1, 'degree': 4, 'epsilon': 0.8, 'kernel': 'poly'}
0.6043553180303636 {'C': 25, 'degree': 4, 'epsilon': 0.8, 'kernel': 'poly'}
0.6031393761401793 {'C': 25, 'degree': 4, 'epsilon': 0.75, 'kernel': 'poly'}
0.6031385109268919 {'C': 20, 'degree': 4, 'epsilon': 0.75, 'kernel': 'poly'}
0.6031376456463644 {'C': 15, 'degree': 4, 'epsilon': 0.75, 'kernel': 'poly'}
0.603136780372397 {'C': 10, 'degree': 4, 'epsilon': 0.75, 'kernel': 'poly'}
0.5987402080876119 {'C': 1, 'degree': 4, 'epsilon': 0.75, 'kernel': 'poly'}
0.5981568009220716 {'C': 20, 'degree': 4, 'epsilon': 0.7, 'kernel': 'poly'}
0.5981553597883185 {'C': 10, 'degree': 4, 'epsilon': 0.7, 'kernel': 'poly'}
0.5981439489239856 {'C': 15, 'degree': 4, 'epsilon': 0.7, 'kernel': 'poly'}
0.5981333670332925 {'C': 25, 'degree': 4, 'epsilon': 0.7, 'kernel': 'poly'}
0.5968821029212972 {'C': 1, 'degree': 4, 'epsilon': 0.7, 'kernel': 'poly'}
0.5925001477792832 {'C': 1, 'degree': 4, 'epsilon': 0.6, 'kernel': 'poly'}
0.5920208116429452 {'C': 25, 'degree': 4, 'epsilon': 0.6, 'kernel': 'poly'}
0.5920207000948442 {'C': 20, 'degree': 4, 'epsilon': 0.6, 'kernel': 'poly'}
0.5920205885444009 {'C': 15, 'degree': 4, 'epsilon': 0.6, 'kernel': 'poly'}
0.5920204770089783 {'C': 10, 'degree': 4, 'epsilon': 0.6, 'kernel': 'poly'}
0.5877161389933874 {'C': 25, 'degree': 4, 'epsilon': 0.65, 'kernel': 'poly'}
0.5877140830489975 {'C': 20, 'degree': 4, 'epsilon': 0.65, 'kernel': 'poly'}
0.5877132984539946 {'C': 15, 'degree': 4, 'epsilon': 0.65, 'kernel': 'poly'}
0.5877120432574239 {'C': 10, 'degree': 4, 'epsilon': 0.65, 'kernel': 'poly'}
0.5877102077477063 {'C': 1, 'degree': 4, 'epsilon': 0.65, 'kernel': 'poly'}
0.587398440041328 {'C': 25, 'degree': 4, 'epsilon': 0.5, 'kernel': 'poly'}
0.5873978365954838 {'C': 20, 'degree': 4, 'epsilon': 0.5, 'kernel': 'poly'}
0.587397233180915 {'C': 15, 'degree': 4, 'epsilon': 0.5, 'kernel': 'poly'}
0.5873966297742281 {'C': 10, 'degree': 4, 'epsilon': 0.5, 'kernel': 'poly'}
0.5873955437872145 {'C': 1, 'degree': 4, 'epsilon': 0.5, 'kernel': 'poly'}
0.5706029990598732 {'C': 25, 'degree': 2, 'epsilon': 0.75, 'kernel': 'poly'}
0.570602939484524 {'C': 20, 'degree': 2, 'epsilon': 0.75, 'kernel': 'poly'}
0.5706028796907244 {'C': 15, 'degree': 2, 'epsilon': 0.75, 'kernel': 'poly'}
0.5706028201795862 {'C': 10, 'degree': 2, 'epsilon': 0.75, 'kernel': 'poly'}
0.5695466405310565 {'C': 1, 'degree': 2, 'epsilon': 0.8, 'kernel': 'poly'}
0.5695465853819102 {'C': 10, 'degree': 2, 'epsilon': 0.8, 'kernel': 'poly'}
0.5695465552601844 {'C': 15, 'degree': 2, 'epsilon': 0.8, 'kernel': 'poly'}
0.5695465244363138 {'C': 20, 'degree': 2, 'epsilon': 0.8, 'kernel': 'poly'}
0.5695464933063024 {'C': 25, 'degree': 2, 'epsilon': 0.8, 'kernel': 'poly'}
0.5635780605921075 {'C': 25, 'degree': 2, 'epsilon': 0.7, 'kernel': 'poly'}
0.563424276623962 {'C': 10, 'degree': 2, 'epsilon': 0.7, 'kernel': 'poly'}
0.5634241095663366 {'C': 15, 'degree': 2, 'epsilon': 0.7, 'kernel': 'poly'}
0.5634239425907728 {'C': 20, 'degree': 2, 'epsilon': 0.7, 'kernel': 'poly'}
0.5629561953202273 {'C': 1, 'degree': 2, 'epsilon': 0.75, 'kernel': 'poly'}
0.5578732170539944 {'C': 25, 'degree': 2, 'epsilon': 0.6, 'kernel': 'poly'}
0.5578731587743669 {'C': 20, 'degree': 2, 'epsilon': 0.6, 'kernel': 'poly'}
0.5578731005055465 {'C': 15, 'degree': 2, 'epsilon': 0.6, 'kernel': 'poly'}
0.5578730422647848 {'C': 10, 'degree': 2, 'epsilon': 0.6, 'kernel': 'poly'}
0.5571221847694247 {'C': 1, 'degree': 2, 'epsilon': 0.6, 'kernel': 'poly'}
0.5562088187341648 {'C': 1, 'degree': 2, 'epsilon': 0.65, 'kernel': 'poly'}
0.5560179003882222 {'C': 10, 'degree': 2, 'epsilon': 0.65, 'kernel': 'poly'}
0.5559909328574477 {'C': 25, 'degree': 2, 'epsilon': 0.65, 'kernel': 'poly'}
0.5559908601989739 {'C': 20, 'degree': 2, 'epsilon': 0.65, 'kernel': 'poly'}
0.5559907875509155 {'C': 15, 'degree': 2, 'epsilon': 0.65, 'kernel': 'poly'}
0.5551950850906641 {'C': 1, 'degree': 2, 'epsilon': 0.5, 'kernel': 'poly'}
0.5551949360771401 {'C': 20, 'degree': 2, 'epsilon': 0.5, 'kernel': 'poly'}
0.5551949137506017 {'C': 10, 'degree': 2, 'epsilon': 0.5, 'kernel': 'poly'}
0.5551948185648544 {'C': 15, 'degree': 2, 'epsilon': 0.5, 'kernel': 'poly'}
0.5551946282092552 {'C': 25, 'degree': 2, 'epsilon': 0.5, 'kernel': 'poly'}
0.5495606256512976 {'C': 1, 'degree': 2, 'epsilon': 0.7, 'kernel': 'poly'}
Randomized Search¶
Randomized Search is another approach to tune hyperparameters. You need to give a range for each hyperparameter. Randomized Search randomly sample from each range of hyperparameter and the optimum values for hyperparameters are achieved based on the highest performance.
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint
from numpy import random
import warnings
warnings.filterwarnings('ignore')
np.random.seed(42)
svm = SVR()
params = {'kernel': ['poly','linear'],'degree': randint(low=1, high=4),
'C':list(random.randint(1,25,size=(100))),
'epsilon':[0.4,0.5,0.6,0.65,0.7,0.75,0.8]}
svm_search_cv = RandomizedSearchCV(svm, params,n_iter=150,
cv=4,scoring="neg_mean_squared_error")
svm_search_cv.fit(X,y)
# Optimum values for the hyperparameters are:
svm_search_cv.best_params_
{'C': 1, 'degree': 2, 'epsilon': 0.7, 'kernel': 'poly'}
cvreslt=svm_search_cv.cv_results_
cvreslt_params=[str(i) for i in cvreslt["params"]]
for mean_score, params in sorted(zip(cvreslt["mean_test_score"], cvreslt_params)):
print(np.sqrt(-mean_score), params)
0.8838835591190869 {'C': 8, 'degree': 3, 'epsilon': 0.4, 'kernel': 'poly'}
0.8838826354911381 {'C': 16, 'degree': 3, 'epsilon': 0.4, 'kernel': 'poly'}
0.8838820582312131 {'C': 21, 'degree': 3, 'epsilon': 0.4, 'kernel': 'poly'}
0.8838819427612681 {'C': 22, 'degree': 3, 'epsilon': 0.4, 'kernel': 'poly'}
0.8838510949763071 {'C': 11, 'degree': 3, 'epsilon': 0.4, 'kernel': 'poly'}
0.8647969484820162 {'C': 2, 'degree': 3, 'epsilon': 0.5, 'kernel': 'poly'}
0.8647968478904856 {'C': 1, 'degree': 3, 'epsilon': 0.5, 'kernel': 'poly'}
0.8548738327354128 {'C': 4, 'degree': 3, 'epsilon': 0.7, 'kernel': 'poly'}
0.8548735955998962 {'C': 6, 'degree': 3, 'epsilon': 0.7, 'kernel': 'poly'}
0.8548733582112923 {'C': 8, 'degree': 3, 'epsilon': 0.7, 'kernel': 'poly'}
0.8548732395343085 {'C': 9, 'degree': 3, 'epsilon': 0.7, 'kernel': 'poly'}
0.8548725280790783 {'C': 15, 'degree': 3, 'epsilon': 0.7, 'kernel': 'poly'}
0.8533994825841431 {'C': 24, 'degree': 3, 'epsilon': 0.8, 'kernel': 'poly'}
0.8533993646182054 {'C': 23, 'degree': 3, 'epsilon': 0.8, 'kernel': 'poly'}
0.8533991286925899 {'C': 21, 'degree': 3, 'epsilon': 0.8, 'kernel': 'poly'}
0.8533803495987885 {'C': 4, 'degree': 3, 'epsilon': 0.8, 'kernel': 'poly'}
0.8533803495987885 {'C': 4, 'degree': 3, 'epsilon': 0.8, 'kernel': 'poly'}
0.852815751689016 {'C': 19, 'degree': 3, 'epsilon': 0.6, 'kernel': 'poly'}
0.852815751689016 {'C': 19, 'degree': 3, 'epsilon': 0.6, 'kernel': 'poly'}
0.8528155372386057 {'C': 16, 'degree': 3, 'epsilon': 0.6, 'kernel': 'poly'}
0.8528153942767351 {'C': 14, 'degree': 3, 'epsilon': 0.6, 'kernel': 'poly'}
0.8515082022345914 {'C': 16, 'degree': 1, 'epsilon': 0.8, 'kernel': 'linear'}
0.8515077184399135 {'C': 24, 'degree': 2, 'epsilon': 0.8, 'kernel': 'linear'}
0.8515077184399135 {'C': 24, 'degree': 3, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514902702313302 {'C': 7, 'degree': 1, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514902702313302 {'C': 7, 'degree': 2, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514460711244022 {'C': 13, 'degree': 1, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514448092763703 {'C': 21, 'degree': 2, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514290453884454 {'C': 4, 'degree': 1, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514123394082993 {'C': 12, 'degree': 1, 'epsilon': 0.8, 'kernel': 'poly'}
0.8514085172904734 {'C': 23, 'degree': 1, 'epsilon': 0.8, 'kernel': 'poly'}
0.8514083348940451 {'C': 18, 'degree': 2, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514081907019314 {'C': 9, 'degree': 1, 'epsilon': 0.8, 'kernel': 'poly'}
0.8514081578778515 {'C': 9, 'degree': 1, 'epsilon': 0.8, 'kernel': 'linear'}
0.8514081382202101 {'C': 8, 'degree': 2, 'epsilon': 0.8, 'kernel': 'linear'}
0.8507499839231185 {'C': 18, 'degree': 3, 'epsilon': 0.75, 'kernel': 'poly'}
0.8489113029997387 {'C': 7, 'degree': 3, 'epsilon': 0.65, 'kernel': 'poly'}
0.8489072194093401 {'C': 17, 'degree': 3, 'epsilon': 0.65, 'kernel': 'poly'}
0.8489050795030306 {'C': 21, 'degree': 3, 'epsilon': 0.65, 'kernel': 'poly'}
0.8489013824763366 {'C': 16, 'degree': 3, 'epsilon': 0.65, 'kernel': 'poly'}
0.8489013824763366 {'C': 16, 'degree': 3, 'epsilon': 0.65, 'kernel': 'poly'}
0.8489012979639533 {'C': 15, 'degree': 3, 'epsilon': 0.65, 'kernel': 'poly'}
0.8489001991900924 {'C': 2, 'degree': 3, 'epsilon': 0.65, 'kernel': 'poly'}
0.8489001991900924 {'C': 2, 'degree': 3, 'epsilon': 0.65, 'kernel': 'poly'}
0.8430268609483316 {'C': 24, 'degree': 1, 'epsilon': 0.75, 'kernel': 'poly'}
0.8430267836007169 {'C': 21, 'degree': 1, 'epsilon': 0.75, 'kernel': 'poly'}
0.8430267059982424 {'C': 18, 'degree': 1, 'epsilon': 0.75, 'kernel': 'poly'}
0.8430265510904139 {'C': 12, 'degree': 1, 'epsilon': 0.75, 'kernel': 'poly'}
0.843026383904745 {'C': 15, 'degree': 3, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430263648192714 {'C': 13, 'degree': 2, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430263552586522 {'C': 12, 'degree': 2, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430263362454073 {'C': 10, 'degree': 2, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430263266832754 {'C': 9, 'degree': 2, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430263075940534 {'C': 7, 'degree': 3, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430262695869413 {'C': 3, 'degree': 3, 'epsilon': 0.75, 'kernel': 'linear'}
0.8430262600361174 {'C': 2, 'degree': 1, 'epsilon': 0.75, 'kernel': 'linear'}
0.8401670604564085 {'C': 20, 'degree': 2, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401670524522259 {'C': 18, 'degree': 3, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401670202885926 {'C': 10, 'degree': 1, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401670202885926 {'C': 10, 'degree': 1, 'epsilon': 0.65, 'kernel': 'linear'}
0.840167016266541 {'C': 9, 'degree': 1, 'epsilon': 0.65, 'kernel': 'linear'}
0.840167016266541 {'C': 9, 'degree': 3, 'epsilon': 0.65, 'kernel': 'linear'}
0.840167012256424 {'C': 8, 'degree': 3, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401669960658033 {'C': 4, 'degree': 1, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401669881266349 {'C': 2, 'degree': 1, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401669881266349 {'C': 2, 'degree': 1, 'epsilon': 0.65, 'kernel': 'linear'}
0.8401669562230698 {'C': 4, 'degree': 1, 'epsilon': 0.65, 'kernel': 'poly'}
0.8401669383669181 {'C': 7, 'degree': 1, 'epsilon': 0.65, 'kernel': 'poly'}
0.8401669205370896 {'C': 10, 'degree': 1, 'epsilon': 0.65, 'kernel': 'poly'}
0.8401669086289526 {'C': 12, 'degree': 1, 'epsilon': 0.65, 'kernel': 'poly'}
0.840166884791506 {'C': 16, 'degree': 1, 'epsilon': 0.65, 'kernel': 'poly'}
0.8401668550237592 {'C': 21, 'degree': 1, 'epsilon': 0.65, 'kernel': 'poly'}
0.8401668550237592 {'C': 21, 'degree': 1, 'epsilon': 0.65, 'kernel': 'poly'}
0.8401668371893947 {'C': 24, 'degree': 1, 'epsilon': 0.65, 'kernel': 'poly'}
0.8399442561957052 {'C': 4, 'degree': 1, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399331236539161 {'C': 14, 'degree': 3, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399331216457674 {'C': 13, 'degree': 1, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399331176381434 {'C': 11, 'degree': 2, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399331136265858 {'C': 9, 'degree': 1, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399331136265858 {'C': 9, 'degree': 2, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399331096150846 {'C': 7, 'degree': 2, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399331096150846 {'C': 7, 'degree': 2, 'epsilon': 0.7, 'kernel': 'linear'}
0.8399329164566691 {'C': 14, 'degree': 1, 'epsilon': 0.7, 'kernel': 'poly'}
0.839932903741658 {'C': 15, 'degree': 1, 'epsilon': 0.7, 'kernel': 'poly'}
0.839932903741658 {'C': 15, 'degree': 1, 'epsilon': 0.7, 'kernel': 'poly'}
0.8399327884996097 {'C': 24, 'degree': 1, 'epsilon': 0.7, 'kernel': 'poly'}
0.837693438419881 {'C': 24, 'degree': 1, 'epsilon': 0.4, 'kernel': 'poly'}
0.8376933602281171 {'C': 18, 'degree': 1, 'epsilon': 0.4, 'kernel': 'poly'}
0.8376932430857206 {'C': 9, 'degree': 1, 'epsilon': 0.4, 'kernel': 'poly'}
0.8376931280051111 {'C': 24, 'degree': 1, 'epsilon': 0.4, 'kernel': 'linear'}
0.8376931280051111 {'C': 24, 'degree': 1, 'epsilon': 0.4, 'kernel': 'linear'}
0.8376931280051111 {'C': 24, 'degree': 2, 'epsilon': 0.4, 'kernel': 'linear'}
0.8376931280051111 {'C': 24, 'degree': 2, 'epsilon': 0.4, 'kernel': 'linear'}
0.8376931279821884 {'C': 23, 'degree': 1, 'epsilon': 0.4, 'kernel': 'linear'}
0.8376931279000669 {'C': 21, 'degree': 2, 'epsilon': 0.4, 'kernel': 'linear'}
0.8376931278508295 {'C': 20, 'degree': 2, 'epsilon': 0.4, 'kernel': 'linear'}
0.8376931278462246 {'C': 19, 'degree': 3, 'epsilon': 0.4, 'kernel': 'linear'}
0.8376931278462246 {'C': 19, 'degree': 3, 'epsilon': 0.4, 'kernel': 'linear'}
0.8376931277416622 {'C': 17, 'degree': 1, 'epsilon': 0.4, 'kernel': 'linear'}
0.8376931277416622 {'C': 17, 'degree': 3, 'epsilon': 0.4, 'kernel': 'linear'}
0.8376931277162444 {'C': 16, 'degree': 3, 'epsilon': 0.4, 'kernel': 'linear'}
0.8376931275248256 {'C': 11, 'degree': 1, 'epsilon': 0.4, 'kernel': 'linear'}
0.8376931274132363 {'C': 8, 'degree': 1, 'epsilon': 0.4, 'kernel': 'linear'}
0.836114881327588 {'C': 6, 'degree': 2, 'epsilon': 0.4, 'kernel': 'linear'}
0.834721474921055 {'C': 15, 'degree': 1, 'epsilon': 0.6, 'kernel': 'linear'}
0.834721474921055 {'C': 15, 'degree': 3, 'epsilon': 0.6, 'kernel': 'linear'}
0.8346667321882687 {'C': 18, 'degree': 1, 'epsilon': 0.6, 'kernel': 'poly'}
0.8346122369668294 {'C': 6, 'degree': 1, 'epsilon': 0.6, 'kernel': 'poly'}
0.8345795443652362 {'C': 12, 'degree': 1, 'epsilon': 0.6, 'kernel': 'poly'}
0.8345788323601626 {'C': 24, 'degree': 2, 'epsilon': 0.6, 'kernel': 'linear'}
0.8345788108326544 {'C': 22, 'degree': 3, 'epsilon': 0.6, 'kernel': 'linear'}
0.8345788000491143 {'C': 21, 'degree': 2, 'epsilon': 0.6, 'kernel': 'linear'}
0.8345787892877505 {'C': 20, 'degree': 3, 'epsilon': 0.6, 'kernel': 'linear'}
0.8345785954019673 {'C': 2, 'degree': 3, 'epsilon': 0.6, 'kernel': 'linear'}
0.8345785846382784 {'C': 1, 'degree': 3, 'epsilon': 0.6, 'kernel': 'linear'}
0.8342275260029224 {'C': 2, 'degree': 2, 'epsilon': 0.4, 'kernel': 'linear'}
0.8342275236177799 {'C': 3, 'degree': 3, 'epsilon': 0.4, 'kernel': 'linear'}
0.8333835304125103 {'C': 22, 'degree': 2, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333810232319543 {'C': 7, 'degree': 1, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333810232319543 {'C': 7, 'degree': 3, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333729911350083 {'C': 14, 'degree': 1, 'epsilon': 0.5, 'kernel': 'poly'}
0.8333728291760423 {'C': 4, 'degree': 1, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333727571141323 {'C': 9, 'degree': 2, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333727571141323 {'C': 9, 'degree': 3, 'epsilon': 0.5, 'kernel': 'linear'}
0.833372742677603 {'C': 10, 'degree': 2, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333727138551118 {'C': 12, 'degree': 2, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333726706233276 {'C': 15, 'degree': 3, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333726706233276 {'C': 15, 'degree': 3, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333726129513541 {'C': 19, 'degree': 1, 'epsilon': 0.5, 'kernel': 'linear'}
0.8333614461826541 {'C': 4, 'degree': 1, 'epsilon': 0.5, 'kernel': 'poly'}
0.570602963233197 {'C': 22, 'degree': 2, 'epsilon': 0.75, 'kernel': 'poly'}
0.5706029155214853 {'C': 18, 'degree': 2, 'epsilon': 0.75, 'kernel': 'poly'}
0.5695466104637095 {'C': 6, 'degree': 2, 'epsilon': 0.8, 'kernel': 'poly'}
0.5695466042179702 {'C': 7, 'degree': 2, 'epsilon': 0.8, 'kernel': 'poly'}
0.5695465180151981 {'C': 21, 'degree': 2, 'epsilon': 0.8, 'kernel': 'poly'}
0.5634752721647158 {'C': 6, 'degree': 2, 'epsilon': 0.7, 'kernel': 'poly'}
0.5634245103837026 {'C': 3, 'degree': 2, 'epsilon': 0.7, 'kernel': 'poly'}
0.5578731704211444 {'C': 21, 'degree': 2, 'epsilon': 0.6, 'kernel': 'poly'}
0.5578730772433353 {'C': 13, 'degree': 2, 'epsilon': 0.6, 'kernel': 'poly'}
0.5578730306429981 {'C': 9, 'degree': 2, 'epsilon': 0.6, 'kernel': 'poly'}
0.5578729956912499 {'C': 6, 'degree': 2, 'epsilon': 0.6, 'kernel': 'poly'}
0.555990918271524 {'C': 24, 'degree': 2, 'epsilon': 0.65, 'kernel': 'poly'}
0.5559907730351292 {'C': 14, 'degree': 2, 'epsilon': 0.65, 'kernel': 'poly'}
0.5551950850906641 {'C': 1, 'degree': 2, 'epsilon': 0.5, 'kernel': 'poly'}
0.5551950850906641 {'C': 1, 'degree': 2, 'epsilon': 0.5, 'kernel': 'poly'}
0.5551948566919108 {'C': 13, 'degree': 2, 'epsilon': 0.5, 'kernel': 'poly'}
0.5551947044022674 {'C': 21, 'degree': 2, 'epsilon': 0.5, 'kernel': 'poly'}
0.5551946472203915 {'C': 24, 'degree': 2, 'epsilon': 0.5, 'kernel': 'poly'}
0.5543606785460717 {'C': 12, 'degree': 2, 'epsilon': 0.4, 'kernel': 'poly'}
0.5495606256512976 {'C': 1, 'degree': 2, 'epsilon': 0.7, 'kernel': 'poly'}
- Home
-
- Prediction of Movie Genre by Fine-tunning GPT
- Fine-tunning BERT for Fake News Detection
- Covid Tweet Classification by Fine-tunning BART
- Semantic Search Using BERT
- Abstractive Semantic Search by OpenAI Embedding
- Fine-tunning GPT for Style Completion
- Extractive Question-Answering by BERT
- Fine-tunning T5 Model for Abstract Title Prediction
- Image Captioning by Fine-tunning ViT
- Build Serverless ChatGPT API
- Statistical Analysis in Python
- Clustering Algorithms
- Customer Segmentation
- Time Series Forecasting
- PySpark Fundamentals for Big Data
- Predict Customer Churn
- Classification with Imbalanced Classes
- Feature Importance
- Feature Selection
- Text Similarity Measurement
- Dimensionality Reduction
- Prediction of Methane Leakage
- Imputation by LU Simulation
- Histogram Uncertainty
- Delustering to Improve Preferential Sampling
- Uncertainty in Spatial Correlation
-
- Machine Learning Overview
- Python and Pandas
- Main Steps of Machine Learning
- Classification
- Model Training
- Support Vector Machines
- Decision Trees
- Ensemble Learning & Random Forests
- Artificial Neural Network
- Deep Neural Network (DNN)
- Unsupervised Learning
- Multicollinearity
- Introduction to Git
- Introduction to R
- SQL Basic to Advanced Level
- Develop Python Package
- Introduction to BERT LLM
- Exploratory Data Analysis
- Object Oriented Programming in Python
- Natural Language Processing
- Convolutional Neural Network
- Publications
