Summary
Given current competition within the market, it is essential to understand customer behaviour, their types, and their interests. Especially in targeted marketing, categorizing and understanding customers is a crucial step in forming effective marketing strategies. By creating customer segments, marketers can focus on one segment at a time and tailor their marketing strategies. For example, you have a hotel business, and you may target couples who have upcoming anniversaries and offer them a special romantic package. In this notebook, first clustering is applied to separate customers into clusters. To avoid suboptimal solution, mini-batch k-means applies multiple times to get average of centroids of clusters. Then based on the mean of features for each clusters, segments are defined. Finally, PCA algorithms is applied to visualize grouped customers.
Python functions and data files to run this notebook are in my Github page.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pandas import DataFrame
import matplotlib as mpl
import time
import os
import random
import warnings
warnings.filterwarnings('ignore')
from functions import* # import require functions to run this notebook
from nbconvert import HTMLExporter
from IPython.display import clear_output
#scikit-learn==0.24.2
from sklearn.decomposition import PCA
from sklearn.datasets import make_blobs
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import StandardScaler
Data Processing¶
All customers are not the same. Customer segmentation groups customers into segments based on specific attributes. Segments are statistically determined based on behavioral features/variables. Customers segmentation can based on customer's activity on a website, their purchases, their returns and so on. This is really helpful to understand what customers need and who they are, so the products can be compatible to each segment. For customer segmentation, it is first required to apply clustering. Clustering separates customers into clusters, where clusters are as different as possible and customers within a cluster are as similar as possible. The clustering algorithm determines the clusters and assigns a cluster label to each customer, indicating membership to cluster 1, 2, ... Customer segmentation applies statistical analysis to all features and see how they rank from one cluster to the next. See schematic illustration below:
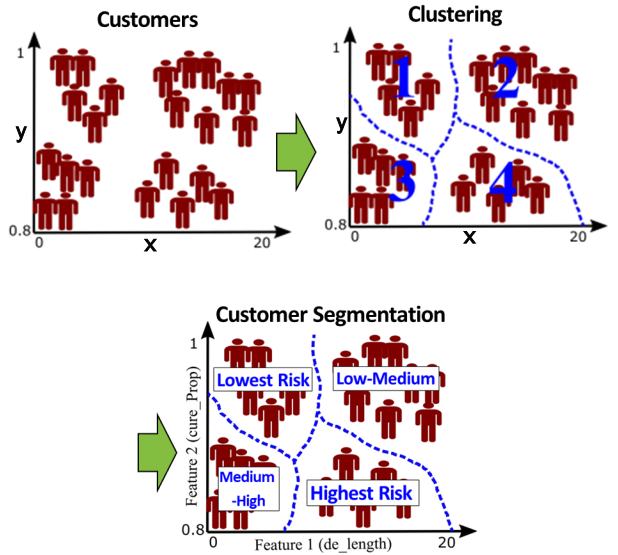
The data for this notebook is downloaded from this page Github. Here are description for each column of this data.
ID: Shows a unique identification of a customer.
Sex: Biological sex (gender) of a customer. In this dataset, there are only 2 different options.
- 0: male
- 1: female
Marital status: Marital status of a customer.
- 0: single
- 1: non-single (divorced / separated / married / widowed)
Age: The age of the customer in years, calculated as current year minus the year of birth of the customer at the time of the creation of the dataset
- 18 Min value (the lowest age observed in the dataset)
- 76 Max value (the highest age observed in the dataset)
Education: Level of education of the customer.
- 0:other / unknown
- 1: high school
- 2: university
- 3: graduate school
Income: Self-reported annual income in US dollars of the customer.
Occupation: Category of occupation of the customer.
- 0: unemployed/unskilled
- 1: skilled employee / official
- 2: management / self-employed / highly qualified employee / officer
Settlement size: The size of the city that the customer lives in.
- 0: small city
- 1: mid-sized city
- 2: big city
Retrieved from medium
#load data
df=pd.read_csv('./Data/segmentation_data.csv', encoding= 'unicode_escape')
df=df.drop(['ID'],axis=1)
features_colums=df.columns
df
| Sex | Marital status | Age | Education | Income | Occupation | Settlement size | |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 67 | 2 | 124670 | 1 | 2 |
| 1 | 1 | 1 | 22 | 1 | 150773 | 1 | 2 |
| 2 | 0 | 0 | 49 | 1 | 89210 | 0 | 0 |
| 3 | 0 | 0 | 45 | 1 | 171565 | 1 | 1 |
| 4 | 0 | 0 | 53 | 1 | 149031 | 1 | 1 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 1995 | 1 | 0 | 47 | 1 | 123525 | 0 | 0 |
| 1996 | 1 | 1 | 27 | 1 | 117744 | 1 | 0 |
| 1997 | 0 | 0 | 31 | 0 | 86400 | 0 | 0 |
| 1998 | 1 | 1 | 24 | 1 | 97968 | 0 | 0 |
| 1999 | 0 | 0 | 25 | 0 | 68416 | 0 | 0 |
2000 rows × 7 columns
font = {'size' : 7}
plt.rc('font', **font)
fig, ax1 = plt.subplots(figsize=(10, 10), dpi= 100, facecolor='w', edgecolor='k')
colors_map = plt.cm.get_cmap('jet')
colors = colors_map(np.linspace(0,0.8,len(features_colums)))
for ir in range(len(features_colums)):
ax1=plt.subplot(4,2,ir+1)
val=df[features_colums[ir]]
EDA_plot.histplt(val,bins=20,title=f'{features_colums[ir]}',xlabl=None,days=False,
ylabl=None,xlimt=None,ylimt=(0,1)
,axt=ax1,nsplit=5,scale=1.02,loc=2,font=9,color=colors[len(features_colums)-ir-1])
plt.subplots_adjust(hspace=0.4)
plt.subplots_adjust(wspace=0.2)
fig.suptitle(f'Histogram of Variables for Synthetic Data', fontsize=16,y=0.96)
plt.show()
# Correlation matrix
font = {'size' : 13}
plt.rc('font', **font)
fig, ax=plt.subplots(figsize=(6, 6), dpi= 110, facecolor='w', edgecolor='k')
corr_array=Correlation_plot.corr_mat(df,
title=f'Correlation Matrix',corr_val_font=12,
titlefontsize=12,xy_title=[1.5,-3],xyfontsize = 10,vlim=[-1, 1],axt=ax)
df.describe()
| Sex | Marital status | Age | Education | Income | Occupation | Settlement size | |
|---|---|---|---|---|---|---|---|
| count | 2000.000000 | 2000.000000 | 2000.000000 | 2000.00000 | 2000.000000 | 2000.000000 | 2000.000000 |
| mean | 0.457000 | 0.496500 | 35.909000 | 1.03800 | 120954.419000 | 0.810500 | 0.739000 |
| std | 0.498272 | 0.500113 | 11.719402 | 0.59978 | 38108.824679 | 0.638587 | 0.812533 |
| min | 0.000000 | 0.000000 | 18.000000 | 0.00000 | 35832.000000 | 0.000000 | 0.000000 |
| 25% | 0.000000 | 0.000000 | 27.000000 | 1.00000 | 97663.250000 | 0.000000 | 0.000000 |
| 50% | 0.000000 | 0.000000 | 33.000000 | 1.00000 | 115548.500000 | 1.000000 | 1.000000 |
| 75% | 1.000000 | 1.000000 | 42.000000 | 1.00000 | 138072.250000 | 1.000000 | 1.000000 |
| max | 1.000000 | 1.000000 | 76.000000 | 3.00000 | 309364.000000 | 2.000000 | 2.000000 |
# Normalize data
scaler = StandardScaler()
df_std=scaler.fit_transform(df)
Mini-Batch K-Means¶
The K-Means is a simple algorithm that can very quickly and efficiently perform clustering. The reliable clusters are often achieved in a few iteration. It starts by randomly placing the centroids for number of clusters (here is 4) and label the instances accordingly. Then update the centroids, label the instances. This process is repeated for multiple iterations until the centroids stop moving.
Another important variant of the K-Means algorithm was proposed in a 2010 paper by David Sculley. Instead of using the full dataset at each iteration, the algorithm is capable of using mini-batches, moving the centroids just slightly at each iteration. This speeds up the algorithm typically by a factor of 3 or 4 and makes it possible to cluster huge datasets that do not fit in memory. Scikit-Learn implements this algorithm in the MiniBatchKMeans class. You can just use this class like the KMeans class.
(Retrieved from Aurélien Géron)
Optimum Number of Clusters¶
Optimum number of clusters can be found by two approaches below:
- Elbow rule
When the inertia drops very quickly but it reaches a number of cluster that decreases much more slowly. The curve has roughly the shape of an arm called “elbow”.
- Silhouette (si·luh·wet) coefficient
A more precise approach (but also more computationally expensive) is to use the silhouette score, which is the mean silhouette coefficient over all the instances. An instance’s silhouette coefficient is equal to (b – a) / max(a, b) where a is the mean distance to the other instances in the same cluster (it is the mean intra-cluster distance), and b is the mean nearest-cluster distance, that is the mean distance to the instances of the next closest cluster (defined as the one that minimizes b, excluding the instance’s own cluster). The silhouette coefficient can vary between -1 and +1: a coefficient close to +1 means that the instance is well inside its own cluster and far from other clusters, while a coefficient close to 0 means that it is close to a cluster boundary, and finally a coefficient close to -1 means that the instance may have been assigned to the wrong cluster.
(Retrieved from Aurélien Géron)
Running clustering for the same dataset for multiple times (say 100 times) with different seeds and shuffled data can lead to significant difference in proportion of clusters even though the majority vote is applied. The main reason is because the algorithm could end to suboptimal solution if data are noisy. This is the major challenge. The realizations for multiple runs of clustering should NOT be very different from each other since it would be problematic to choose one realization. To resolve this issue, the average center of clusters are achieved and used as centroid initialization to run clustering. Solution is summarized as below:
- Run clustering (mini-batch k-mean) multiple times (100)
- Calculate the mean of centroids (mean of 100 realizations for each cluster)
- Use the means as the initial values of the centroids when new running mini-batch k-mean
Stable proportion of clusters are achieved by using this approach.
%%time
nsim=100
inertia_mbat_kmean_,silhouette_mbat_kmean_=[],[]
for ii in range(nsim):
n_clus_mbat_kmean,time_mbat_kmean,inertia_mbat_kmean,silhouette_mbat_kmean=kmean_eda(data=df_std,k_start=2,k_end=8,
kint=1,minibatch=True,batch_size=500+random.randint(5, 1000),silhouette=True, seed=32+ii)
inertia_mbat_kmean_.append(inertia_mbat_kmean)
silhouette_mbat_kmean_.append(silhouette_mbat_kmean)
# Calculate mean of silhouette score for multiple run
mean_sl=np.zeros((nsim))
for ii in range(nsim):
tmp2=silhouette_mbat_kmean_[ii]
mean_sl=[(mean_sl[i]+tmp2[i])/(2) for i in range (len(tmp2))]
Wall time: 1min 57s
font = {'size' :15}
plt.rc('font', **font)
fig=plt.figure(figsize=(12, 10), dpi= 100, facecolor='w', edgecolor='k')
ax1=plt.subplot(2,1,1)
for ii in range(nsim):
plt.plot(n_clus_mbat_kmean,inertia_mbat_kmean_[ii],linewidth=1,color='gray',markeredgecolor='k')
plt.xticks(np.arange(1,10),rotation=0,y=0.0, fontsize=15)
plt.text(7.5, 8000, 'n='+str(len(df_std)), ha = 'center',fontsize=20,bbox=dict(facecolor='k', alpha=0.2))
plt.xlim(2,8)
plt.grid(True,which="both",ls="-",linewidth=0.5)
plt.title(f'Number of Clusters (k) vs. Inertia (Mean square Distance) for {nsim} Runs')
plt.xlabel('Number of Clusters (k)',labelpad=14)
plt.ylabel('Inertia')
ax2=plt.subplot(2,1,2)
for ii in range(nsim):
plt.plot(n_clus_mbat_kmean,silhouette_mbat_kmean_[ii],
markersize=8.5,linewidth=1,color='gray',markeredgecolor='k')
plt.plot(n_clus_mbat_kmean,mean_sl, marker='o', label=f'Mean of {nsim} Runs',
markersize=8.5,color='r',linewidth=3,markeredgecolor='k')
plt.grid(True,which="both",ls="-",linewidth=0.5)
plt.title(f'Number of Clusters (k) vs. Silhouette Score for {nsim} Runs')
plt.xlabel('Number of Clusters (k)',labelpad=12)
plt.ylabel('Silhouette score')
plt.axvline(x=4,color='k',linewidth=4,linestyle='--')
plt.legend(loc=4,ncol=1,markerscale=1.0,fontsize=13)
plt.xticks(np.arange(1,8),rotation=0,y=0.0, fontsize=15)
plt.xlim(2,7)
plt.text(4,0.22, 'Optimum k=4',fontsize=15,color='k',
fontweight='bold',style='oblique', ha='center',
va='top', wrap=True,bbox=dict(facecolor='w', alpha=1,pad=5))
plt.ylim(0.2,0.28)
plt.subplots_adjust(wspace=0.12)
plt.subplots_adjust(hspace=0.4)
plt.show()
An even more informative visualization is obtained when you plot every instance’s silhouette coefficient, sorted by the cluster they are assigned to and by the value of the coefficient.
The vertical dashed lines represent the silhouette score for each number of clusters. When most of the instances in a cluster have a lower coefficient than this score (i.e., if many of the instances stop short of the dashed line, ending to the left of it), then the cluster is rather bad since this means its instances are much too close to other clusters. We can see that when k=3 and when k=6, we get bad clusters.
kmeans_per_k = [MiniBatchKMeans(n_clusters=k,batch_size=500,random_state=42).fit(df_std) for k in range(3, 7)]
silhouette_scores = [silhouette_score(df_std, model.labels_) for model in kmeans_per_k]
font = {'size' :13 }
plt.rc('font', **font)
fig=plt.figure(figsize=(11, 9), dpi= 80, facecolor='w', edgecolor='k')
for k in (3, 4, 5, 6):
plt.subplot(2, 2, k - 2)
y_pred = kmeans_per_k[k - 3].labels_
silhouette_coefficients = silhouette_samples(df_std, y_pred)
padding = len(df_std) // 30
pos = padding
ticks = []
for i in range(k):
coeffs = silhouette_coefficients[y_pred == i]
coeffs.sort()
color = mpl.cm.Spectral(i / k)
plt.fill_betweenx(np.arange(pos, pos + len(coeffs)), 0, coeffs,
facecolor=color, edgecolor=color, alpha=0.7)
ticks.append(pos + len(coeffs) // 2)
pos += len(coeffs) + padding
plt.gca().yaxis.set_major_locator(FixedLocator(ticks))
plt.gca().yaxis.set_major_formatter(FixedFormatter(range(k)))
if k in (3, 5):
plt.ylabel("Cluster")
if k in (5, 6):
plt.gca().set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
plt.xlabel("Silhouette Coefficient", fontsize=15)
else:
plt.gca().set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
#plt.tick_params(labelbottom=False)
plt.axvline(x=silhouette_scores[k - 3], color="k", linestyle="--",lw=4)
plt.title(f"k={k} (Silhouette={np.round(silhouette_scores[k - 3],3)})", fontsize=19)
plt.grid(True,which="both",ls="-",linewidth=0.2)
plt.xlim((-0.1, 0.8))
plt.subplots_adjust(wspace=0.2)
plt.subplots_adjust(hspace=0.3)
plt.show()
%%time
# batch kmeans
start_time = time.time()
kmeans_batch = MiniBatchKMeans(n_clusters=4,batch_size=1000)
kmeans_batch.fit_predict(df_std)
km_batch_pred= kmeans_batch.labels_
#km_batch_score=silhouette_score(df_std, km_batch_pred)
#km_batch_pred= (pd.Series(km_batch_pred).value_counts()/len(km_batch_pred)).to_dict()
Wall time: 65.8 ms
Run Clustering Multiple Times¶
Multiple Clustering Random Centroid Initialization¶
############# Rerun the clustering for multiple times #############
nlucter=4
features_center=[]
cluster_proportion=[]
pred_sim=[]
label1=['cluster1','cluster2','cluster3','cluster4']
label2=label1
ir=0
i_it=0
while ir<nsim:
if ir==0:
print(f'Working on Realization {ir+1}')
tmp1, tmp2, pred_first=batch_kmean_multiple(df,k=nlucter,random_seed=34+i_it,
init='k-means++',n_init=3,max_iter=100,batch_size=1000)
pred_sim.append(pred_first)
pred_first=pred_first[['CustomerID','cluster']]
features_center.append(tmp1)
cluster_proportion.append(tmp2)
ir+=1
i_it+=1
else:
try:
print('')
print(f'Working on Realization {ir+1}')
tmp1_, tmp2_, pred=batch_kmean_multiple(df,k=nlucter,random_seed=34+i_it,
init='k-means++',n_init=3,max_iter=100,batch_size=1000)
_,_,_,rank_order=Flow_old_new_cluster(pred_first,pred,label1,label2,clm1_1='CustomerID', clm1_2='cluster',
clm2_1='CustomerID', clm2_2='cluster',print_=False,nlcuster=4)
print(rank_order)
tmp2_1=pd.Series([tmp2_[i] for i in rank_order],index=label1)
pred_sim.append(pred)
features_center.append([tmp1_[k] for k in [int(i[-1])-1 for i in rank_order]])
cluster_proportion.append(tmp2_1)
ir+=1
i_it+=1
except ValueError:
print('This Realization is not accepted due to fail majority vote.')
i_it+=1
clear_output(wait=False)
font = {'size' : 11}
plt.rc('font', **font)
fig, ax1 = plt.subplots(figsize=(9, 8), dpi= 140, facecolor='w', edgecolor='k')
############# Plot the proportion of clusters #############
clmns=df.columns
ax1=plt.subplot(2,1,1)
jet= plt.get_cmap('jet')
colors_map = plt.cm.get_cmap('jet')
colors = colors_map(np.linspace(0,0.8,nsim))
ind_features_center=np.arange(len(clmns))
cluster=['cluster1','cluster2','cluster3','cluster4']
for i in range(0,nsim):
val=[cluster_proportion[i][f'cluster{j+1}'] for j in range(nlucter)]
plt.plot(val, color=colors[i])
plt.xticks(np.arange(len(cluster)), cluster,rotation=0,fontsize=12,y=0.02)
plt.ylabel('Proportion of each Cluster',fontsize=11)
plt.title(f'Proportion of each Cluster for {nsim} Runs',fontsize=14)
plt.text(2.5, 0.45, f'n={len(df)}', ha = 'center',fontsize=15,bbox=dict(facecolor='k', alpha=0.2))
ax1.grid(linewidth='0.05')
ax1.xaxis.grid(color='k', linestyle='-', linewidth=0.15) # horizontal lines
plt.ylim(0,0.55)
plt.show()
Centroids of Realizations¶
############# Plot the centeroid of clusters for realizations #############
font = {'size' : 9}
plt.rc('font', **font)
fig, ax1 = plt.subplots(figsize=(9, 8), dpi= 140, facecolor='w', edgecolor='k')
############# Plot the proportion of clusters #############
ax1=plt.subplot(2,1,1)
ind_features_center=np.arange(len(clmns))
colors = [(0.0, 0.3, 1.0, 1.0),
(0.16129032258064513, 1.0, 0.8064516129032259, 1.0),
(0.8064516129032256, 1.0, 0.16129032258064513, 1.0),
(1.0, 0.40740740740740755, 0.0, 1.0)]
# name of clusters
cent_lbl=[int(i[-1])-1 for i in label1]
for i in range(0,nsim):
ir=0
if i==0:
for j in cent_lbl:
plt.plot(features_center[i][j], label=f'Cluster {ir+1}',color=colors[ir])
ir+=1
else:
for j in cent_lbl:
plt.plot(features_center[i][j],color=colors[ir])
ir+=1
mean_centr=np.zeros((len(clmns)))
final_tmp_sim=[]
for isim in range(nsim):
tmp_sim=[]
for ifeat in range(len(clmns)):
tmp=[]
for iclus in cent_lbl:
tmp.append(features_center[isim][iclus][ifeat])
tmp_sim.append(np.mean(tmp))
final_tmp_sim.append(tmp_sim)
mean_centr=[mean_centr[i]+tmp_sim[i]/nsim for i in range (len(tmp_sim))]
#plt.plot(mean_centr, 's--',color='k',markersize=7,linewidth=4,label='Mean')
plt.xticks(ind_features_center, clmns,rotation=90,fontsize=11,y=0.00)
plt.ylabel('Values for Centroid of Clusters',fontsize=11)
plt.title(f'Centroid of Clusters for {nsim} Runs',fontsize=14)
plt.text(0.2, 2.0, f'n={len(df)}', ha = 'center',fontsize=14,bbox=dict(facecolor='k', alpha=0.2))
ax1.grid(linewidth='0.1')
plt.ylim(-2.,2.5)
legend=plt.legend(ncol=2,loc=1,fontsize=9,framealpha =1)
plt.show()
Calculate Mean of Centroids¶
############# Calculate the mean of centeroid for clusters of multiple realizations #############
font = {'size' : 9}
plt.rc('font', **font)
fig, ax1 = plt.subplots(figsize=(9, 8), dpi= 140, facecolor='w', edgecolor='k')
############# Plot the proportion of clusters #############
ax1=plt.subplot(2,1,1)
mean_cluster1=np.zeros((len(clmns)))
mean_cluster2=np.zeros((len(clmns)))
mean_cluster3=np.zeros((len(clmns)))
mean_cluster4=np.zeros((len(clmns)))
final_tmp_sim=[]
for isim in range(nsim):
cluster1=features_center[isim][cent_lbl[0]]
cluster2=features_center[isim][cent_lbl[1]]
cluster3=features_center[isim][cent_lbl[2]]
cluster4=features_center[isim][cent_lbl[3]]
mean_cluster1=[mean_cluster1[i]+cluster1[i]/nsim for i in range (len(cluster1))]
mean_cluster2=[mean_cluster2[i]+cluster2[i]/nsim for i in range (len(cluster2))]
mean_cluster3=[mean_cluster3[i]+cluster3[i]/nsim for i in range (len(cluster3))]
mean_cluster4=[mean_cluster4[i]+cluster4[i]/nsim for i in range (len(cluster4))]
centr_init=np.concatenate((np.array(mean_cluster1),
np.array(mean_cluster2),
np.array(mean_cluster3),
np.array(mean_cluster4),
),axis=0).reshape(nlucter,len(clmns))
plt.plot(mean_cluster1,linewidth=3, label='Mean for Cluster 1',color=colors[0])
plt.plot(mean_cluster2,linewidth=3, label='Mean for Cluster 2',color=colors[1])
plt.plot(mean_cluster3,linewidth=3, label='Mean for Cluster 3',color=colors[2])
plt.plot(mean_cluster4,linewidth=3, label='Mean for Cluster 4',color=colors[3])
plt.xticks(ind_features_center, clmns,rotation=90,fontsize=11,y=0.02)
plt.ylabel('Values for Centroid of Clusters',fontsize=11)
plt.title(f'Mean of Features for Center of Each Cluster',fontsize=14)
plt.text(0.2, 2.0, f'n={len(df)}', ha = 'center',fontsize=14,bbox=dict(facecolor='k', alpha=0.2))
ax1.grid(linewidth='0.1')
plt.ylim(-2.,2.5)
legend=plt.legend(ncol=2,loc=1,fontsize=9,framealpha =1)
plt.show()
## Save the centriods in csv file
#pd_centr_init=pd.DataFrame(centr_init,columns=clmns)
#pd_centr_init['Cluster']=pd_centr_init.index
#pd_centr_init.to_csv(path_centr_init,index = False)
Multiple Clustering with Centroid Initialization (Mean of Centroids)¶
nlucter=4
cluster_proportion=[]
pred_sim=[]
for i in range(0,nsim):
print(f'Working on Realization {i+1}')
tmp1, tmp2, pred=batch_kmean_multiple(df,k=nlucter, init=centr_init,random_seed=34+i,
n_init=3,max_iter=100,batch_size=1000)
pred_sim.append(pred)
pred_first=pred[['CustomerID','cluster']]
features_center.append(tmp1)
cluster_proportion.append(tmp2)
clear_output(wait=False)
font = {'size' : 11}
plt.rc('font', **font)
fig, ax1 = plt.subplots(figsize=(9, 8), dpi= 140, facecolor='w', edgecolor='k')
############# Plot the proportion of clusters #############
clmns=df.columns
ax1=plt.subplot(2,1,1)
jet= plt.get_cmap('jet')
colors_map = plt.cm.get_cmap('jet')
colors = colors_map(np.linspace(0,0.8,nsim))
ind_features_center=np.arange(len(clmns))
cluster=['cluster1','cluster2','cluster3','cluster4']
for i in range(0,nsim):
val=[cluster_proportion[i][f'cluster{j+1}'] for j in range(nlucter)]
plt.plot(val, color=colors[i])
plt.xticks(np.arange(len(cluster)), cluster,rotation=0,fontsize=12,y=0.02)
plt.ylabel('Proportion of each Cluster',fontsize=11)
plt.title(f'Proportion of each Cluster for {nsim} Runs With Fixed Centroids',fontsize=14)
plt.text(2.5, 0.45, f'n={len(df)}', ha = 'center',fontsize=15,bbox=dict(facecolor='k', alpha=0.2))
ax1.grid(linewidth='0.05')
ax1.xaxis.grid(color='k', linestyle='-', linewidth=0.15) # horizontal lines
plt.ylim(0,0.55)
plt.show()
Customer segmentation¶
Customer segmentation is the process of dividing customers into groups based on common characteristics, which allows companies to market each group effectively and appropriately.
Given current competition within the market, it is essential to understand customer behaviour, their types, and their interests. Especially in targeted marketing, categorizing and understanding customers is a crucial step in forming effective marketing strategies. By creating customer segments, marketers can focus on one segment at a time and tailor their marketing strategies. For example, you have a hotel business, and you may target couples who have upcoming anniversaries and offer them a special romantic package.
Overall, customer segmentation is a key for successful targeted marketing, with which you can target specific groups of customers with different promotions, pricing options, and product placement that catch the interests of the target audience in the most cost-effective way [2].
# Choose one clustering realization
dfacc=pred_sim[0].copy()
# Name of clusters
cluster=['cluster1','cluster2','cluster3','cluster4']
clust_per=dfacc['cluster'].value_counts(normalize = True)
val=[clust_per[cluster[i]] for i in range(len(cluster))]
font = {'size' :8 }
plt.rc('font', **font)
fig=plt.figure(figsize=(6, 5), dpi= 200, facecolor='w', edgecolor='k')
ax1=plt.subplot(2,1,1)
jet= plt.get_cmap('jet')
colors = [(0.0, 0.3, 1.0, 1.0),
(0.16129032258064513, 1.0, 0.8064516129032259, 1.0),
(0.8064516129032256, 1.0, 0.16129032258064513, 1.0),
(1.0, 0.40740740740740755, 0.0, 1.0)]
ind=np.arange(len(clust_per))
ax1.bar(ind, val,width=0.55,lw = 1.0, align='center', alpha=1, ecolor='black',
edgecolor='k',capsize=10,color=colors)
ax1.grid(linewidth='0.05')
ax1.xaxis.grid(color='k', linestyle='-', linewidth=0.15) # horizontal lines
plt.text(2.5, 0.5, f'n={len(dfacc)}', ha = 'center',fontsize=10.,bbox=dict(facecolor='k', alpha=0.2))
plt.title('Percentage of 4 Clusters',fontsize=11)
plt.ylabel('Percentage (%)',fontsize=8)
plt.text(-0.15, val[0]+0.01,"{0:.1f}%".format(val[0]*100),fontsize=9.5)
plt.text(0.90, val[1]+0.01,"{0:.1f}%".format(val[1]*100),fontsize=9.5)
plt.text(1.88, val[2]+0.01,"{0:.1f}%".format(val[2]*100),fontsize=9.5)
plt.text(2.88, val[3]+0.01,"{0:.1f}%".format(val[3]*100),fontsize=9.5)
plt.ylim(0,0.65)
plt.gca().yaxis.set_major_formatter(PercentFormatter(1))
plt.xticks(ind, cluster,rotation=0,fontsize=9,y=0.015)
plt.show()
# Mean of clusters for each feature
Clusters_mean=dfacc.drop(['CustomerID'],axis=1).groupby(['cluster']).mean()
Features=list(Clusters_mean.columns)
ind_features=np.arange(len(Features))
# Plot ranking of the means for clusters
scaler = StandardScaler()
Clusters_agg_scale=scaler.fit_transform(Clusters_mean)
array_val=Clusters_mean.to_numpy()
nx=len(Clusters_mean.columns)
ny=4
Var1a=np.zeros((ny,nx))+np.nan
for j in range(ny):
for i in range(nx):
Var1a[j,i]=Clusters_agg_scale[j,i]
font = {'size' : 9}
plt.rc('font', **font)
fig, ax1 = plt.subplots(figsize=(8, 8), dpi= 140, facecolor='w', edgecolor='k')
ax1=plt.subplot(2,1,1)
plt.title(f'Mean of Features for each Cluster',fontsize=13)
cluster=['cluster1: standard', 'cluster2: well-off', 'cluster3: fewer-opportunities', 'cluster4: career focused']
im = plt.imshow(Var1a, cmap='summer',vmin=-1.1,vmax=1.1,
origin='lower',aspect=1, interpolation='none')
for (j, i), _ in np.ndenumerate(Var1a):
label = '{:0.2f}'.format(array_val[j,i])
ax1.text(i,j,label,ha='center',va='center', fontsize=9)
plt.xticks(ind_features, Features,rotation=90,fontsize=9,y=0.02)
plt.yticks(np.arange(0,4), cluster,rotation=0,fontsize=10,y=0.02)
cbaxe_ = fig.add_axes([0.85, 0.61, 0.023, 0.19])
cbar=fig.colorbar(im,cax=cbaxe_,shrink=0.7,orientation='vertical',label='Low High')
cbar.set_ticks([])
plt.show()
font = {'size' : 12}
plt.rc('font', **font)
fig, ax=plt.subplots(figsize=(20, 6), dpi= 100, facecolor='w', edgecolor='k')
ax=plt.subplot(1,2,1)
cmap = plt.cm.rainbow
norm = BoundaryNorm(np.arange(-0.5, 4, 1), cmap.N)
# Apply PCA
pca = PCA(n_components = 2)
X2D = pca.fit_transform(df_std)
sc=ax.scatter(X2D[:, 1], X2D[:, 0],c=km_batch_pred, cmap=cmap, norm=norm, s=40, edgecolor='k')
ax.set_xlabel("$PC2$", fontsize=18)
ax.set_ylabel("$PC1$", fontsize=18, rotation=0)
#plt.gca().set_aspect('1')
ax.set_title('PCA for Customer Segmentatiom',fontsize=17, y=1)
cbar = plt.colorbar(sc,orientation='vertical',shrink=0.9)
cbar.set_ticks([0., 1., 2., 3.])
cluster=['standard', ' well-off', 'fewer-opportunities', 'career focused']
cbar.set_ticklabels(cluster)
#plt.xlim((-0.9, 0.9))
#plt.ylim((-0.8, 0.8))
ax.grid(True, linewidth=0.35)
plt.show()
- Home
-
- Prediction of Movie Genre by Fine-tunning GPT
- Fine-tunning BERT for Fake News Detection
- Covid Tweet Classification by Fine-tunning BART
- Semantic Search Using BERT
- Abstractive Semantic Search by OpenAI Embedding
- Fine-tunning GPT for Style Completion
- Extractive Question-Answering by BERT
- Fine-tunning T5 Model for Abstract Title Prediction
- Image Captioning by Fine-tunning ViT
- Build Serverless ChatGPT API
- Statistical Analysis in Python
- Clustering Algorithms
- Customer Segmentation
- Time Series Forecasting
- PySpark Fundamentals for Big Data
- Predict Customer Churn
- Classification with Imbalanced Classes
- Feature Importance
- Feature Selection
- Text Similarity Measurement
- Dimensionality Reduction
- Prediction of Methane Leakage
- Imputation by LU Simulation
- Histogram Uncertainty
- Delustering to Improve Preferential Sampling
- Uncertainty in Spatial Correlation
-
- Machine Learning Overview
- Python and Pandas
- Main Steps of Machine Learning
- Classification
- Model Training
- Support Vector Machines
- Decision Trees
- Ensemble Learning & Random Forests
- Artificial Neural Network
- Deep Neural Network (DNN)
- Unsupervised Learning
- Multicollinearity
- Introduction to Git
- Introduction to R
- SQL Basic to Advanced Level
- Develop Python Package
- Introduction to BERT LLM
- Exploratory Data Analysis
- Object Oriented Programming in Python
- Natural Language Processing
- Convolutional Neural Network
- Publications
