Introduction
We are inspired by birds to fly but not exactly doing the same as birds do; planes do not flap their wings. This is the key for Artificial Neural Network (ANN). ANN looks at the human brain’s architecture to build an intelligent machine. However, ANN has gradually become quite different from the biological term. ANN is the very core of Deep Learning. Deep Learning usually involves much more successive layers of representations. It is a major field of Machine Learning for tackling very complex problems that Machine Learning is unable to resolve such as classifying billions of images, speech recognition, computer vision. Deep Learning requires big data in order to receive higher performance than Machine Learning and ANN.
How ANN Works¶
The Figure below shows a simple ANN architecture. It consists of input layers, hidden layer and output layer. Input layer is number of futures in training set. Hidden layer is made up of neurons; here we have two neurons, and final layer is output layer, which is number of target for each training instance. When all the neurons in a layer are connected to every neuron in the previous layer, it is called a fully connected layer or a dense layer. A bias neuron is also considered for hidden layer and output layer.
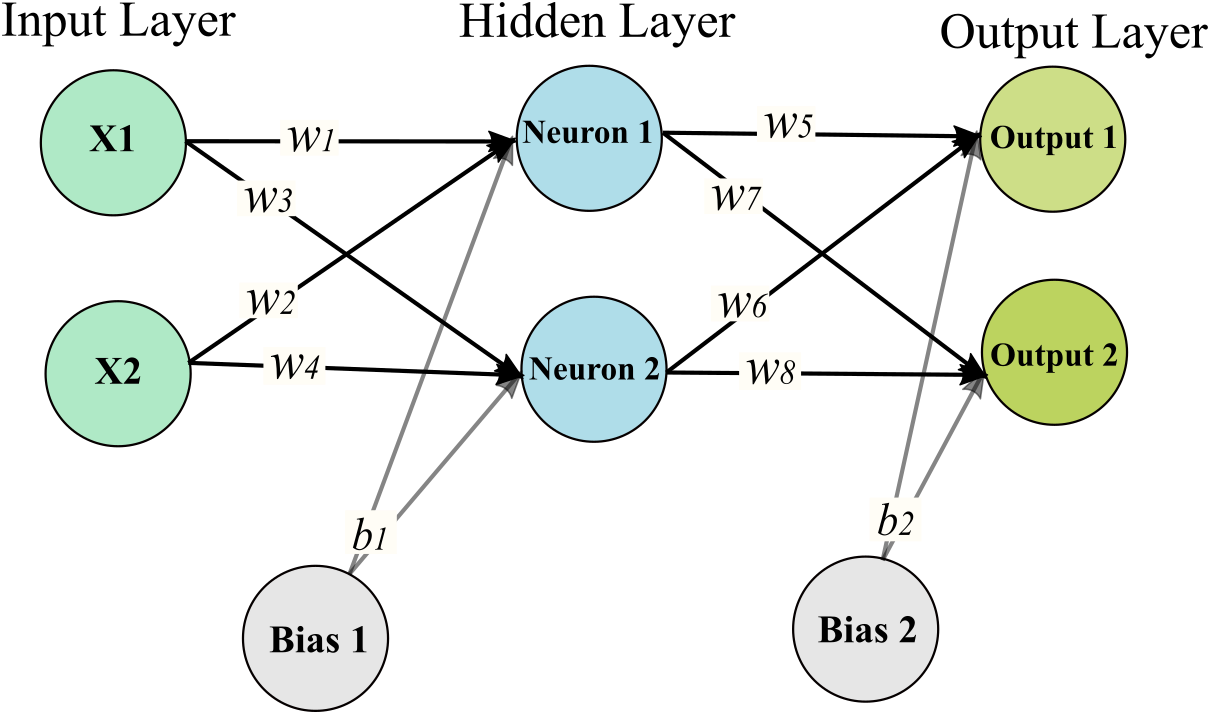
The outputs of a layer of artificial neurons for several instances at once is calculated by:
$O_{\mathbf{w,b}}(\mathbf{x})=\varphi(\mathbf{x}\mathbf{w}+\mathbf{b})$
- X is the matrix of input features.
- W is the connection weights for the neurons except the bias neuron.
- b is the all weights for biased neurons.
- $\varphi$ is a function called activation function.
For the ANN architecture above: $\mathbf{x}=x_{1},x_{2}$, $\mathbf{w}=w_{1},w_{2},w_{3},w_{4},w_{5},w_{6},w_{7},w_{8}$ and $\mathbf{b}=b1_{N1},b1_{N2},b2_{O1},b2_{O2}$.
The weights $\mathbf{w}$ and $\mathbf{b}$ should be optimized by minimizing the calculated error between the calculated output from ANN ($O_{\mathbf{w,b}}(\mathbf{x}$) and actual values. This can be done by backpropagation algorithm; it is simply Gradient Descent discussed before. Backpropagation algorithm applies two passes through the network (one forward, one backward) to calculate the gradient of the network’s error with regards to every single weight. It measures how much each weight and bias term should be tweaked in order to mitigate the error from the actual values. After computing the gradients, simple Gradient Descent is applied by iterating over the entire network until the network converges to the solution.
Lets discuss this approach in more details as below:
1- One mini-batch (mini-batch discussed in previous lecture ) is applied at the time. For example, random selection of 32 training instances can be applied each time. As we discussed before, each iteration is called epoch.
2- Each mini-batch is passed to the first hidden layer. The output of all the neurons in the first layer is calculated and then pass on to the next layer; the output of all the neurons in the new layer are computed and passed again to the next layer. This process is repeated until reaching to the output layer. This is the forward pass. All the weights for the unknown weights and bias terms are randomly generated in this step.
3- Next step is to calculate the ANN output error by using a cost function such as mean square error.
4- Then, the contribution of each parameter (weight) to the error is calculated. This step can be fast and precise by applying chain rule. It starts from the last hidden layer; the chain rule is repeated again until reaching to the input layer. By going through this reverse pass, the error gradient across all the connection weights in the network is efficiently measured: the error gradient is propagated backward through the network. That is why it is called backpropagation.
5- Finally, the algorithm goes through multiple Gradient Descent step to optimize all weights and biases in ANN using the error gradients.
In order to have higher performance for very complex problem and achieve non-linear relations; an activation function $\varphi$ should be used. Since $\mathbf{x}\mathbf{w}+\mathbf{b}$ is a linear transformation, we need some non-linearity between layers to solve complex problems, otherwise even using very deep network will be inefficient.
The common activation functions are:
1- Rectified Linear Unit function: ReLU(z) = max(0, z). Although its derivative is 0 for z<0, ReLU is the fastest and most popular one activation function.
2- Logistic Regression: $\frac{1}{1+e^{-z}}$
3-Tangent function: tanh(z)
See the following plots for these activation function with the derivate of each function:
from matplotlib.colors import ListedColormap
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from numpy import random
import warnings
warnings.filterwarnings('ignore')
font = {'size' : 12}
plt.rc('font', **font)
fig = plt.subplots(figsize=(13.0, 4.5), dpi= 90, facecolor='w', edgecolor='k')
z1 = np.linspace(-4, 4, 100)
#
def sgd(y):
return 1 / (1 + np.exp(-y))
def relu(y):
return np.maximum(0, y)
def drivtve(f, y):
return (f(z1 + 0.000001) - f(z1 - 0.000001))/(2 * 0.000001)
#
plt.subplot(1,2,1)
plt.plot(z1, sgd(z1), "b--", linewidth=2, label="Sigmoid")
plt.plot(z1, np.tanh(z1), "r-", linewidth=2, label="Tanh")
plt.plot(z1, relu(z1), "g-.", linewidth=4, label="ReLU")
plt.grid(True)
plt.legend(loc=4, fontsize=14)
plt.title("Activation functions", fontsize=14)
plt.ylim(-1,1)
plt.subplot(1,2,2)
plt.plot(z1, drivtve(sgd, z1), "b--", linewidth=2, label="Sigmoid")
plt.plot(z1, drivtve(np.tanh, z1), "r-", linewidth=2, label="Tanh")
plt.plot(z1, drivtve(relu, z1), "g-.", linewidth=4, label="ReLU")
plt.grid(True)
plt.title("Derivative of each Activation Function ", fontsize=14)
plt.show()
Lets apply ANN for a simple example below. Assume for one training instance, we have the value X1=0.05, X2= 0.10 for features X1 and X2, respectively. And we have two outputs 0.01 and 0.99. The activation function is logistic regression. First, the weights $w_{1},w_{2},w_{3},w_{4},w_{5},w_{6},w_{7},w_{8}$ and $b1_{N1},b1_{N2},b2_{O1},b2_{O2}$ are randomly generate between 0 to 1 as below:
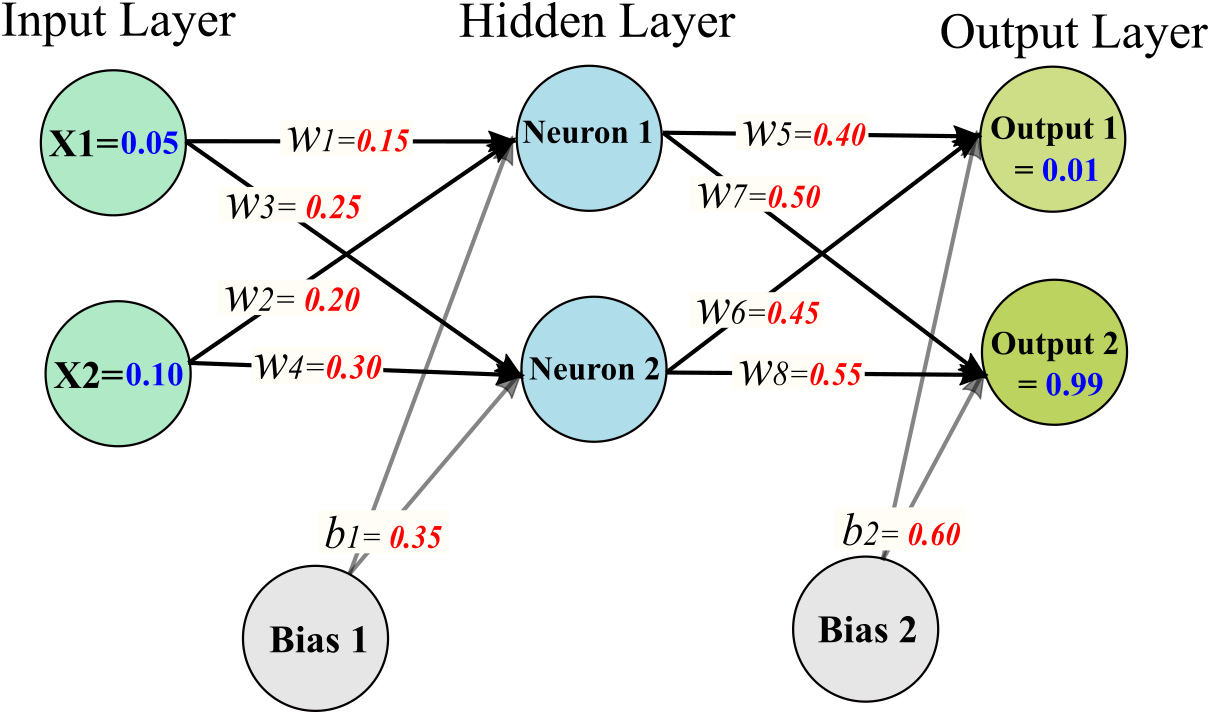
The Forward Pass¶
Neuron 1:
$z_{N1}=x_{1}*w_{1}+x_{2}*w_{2}+b1_{N1}*1= 0.05*0.15+0.1*0.2+0.35*1 =0.3775$.
$ out_{N1}=\frac{1}{1+e^{-z_{N1}}}=0.593269992$
Neuron 2:
$z_{N2}=x_{1}*w_{3}+x_{2}*w_{4}+b1_{N2}*1= 0.05*0.25+0.1*0.3+0.35*1 =0.39249$.
$ out_{N2}=\frac{1}{1+e^{-z_{N2}}}=0.596884378$
Output 1:
$z_{O1}=out_{N1}*w_{5}+out_{N2}*w_{6}+b2_{O1}*1= 0.593269992*0.4+0.596884378*0.45+0.60*1 =1.1059059667$.
$ out_{O1}=\frac{1}{1+e^{-z_{O1}}}=0.75136507$
Output 2:
$z_{O2}=out_{N1}*w_{7}+out_{N2}*w_{8}+b2_{O2}*1= 0.593269992*0.5+0.596884378*0.55+0.60*1 =1.2249214039$.
$ out_{O2}=\frac{1}{1+e^{-z_{O2}}}=0.772928465$
We calculated Output 1 and Output 2, so the mean square error can be calculated as $MSE=\frac{1}{2}\sum_{i=1}^{2} (Target_{i}-Predicted_{i})^{2}=\frac{1}{2}((0.01-0.75136507)^{2}+(0.99-0.772928465)^{2})=0.298371109$.
The Backwards Pass¶
The main aim of backpropagation is to update each the weight in the ANN to make the calculated outputs ($ out_{O1}$,$ out_{O2}$) close to the target values (0.01 and 0.99) by minimizing the error ($MSE$).
Lets do it for $w_{5}$. We want to know how much a very little change in $w_{5}$ impacts $MSE$. So, we should calculate the partial derivative of MSE with respect to $w_{5}$. It is also called the gradient with respect to $w_{5}$: $\frac{\partial MSE}{\partial w_{5}}$. This partial derivative can be calculated by using chain rule:
$\Large \frac{\partial MSE}{\partial w_{5}}= \frac{\partial MSE}{\partial out_{O1}}\times \frac{\partial out_{O1}}{\partial z_{O1}}\times \frac{\partial z_{O1}}{\partial w_{5}}$
Each partial derivative can be calculated as:
$\frac{\partial MSE}{\partial out_{O1}} \rightarrow MSE=\frac{1}{2} \sum_{i=1}^{2} (Target_{out_{Oi}}-out_{Oi})^{2} \,\,\,\,\,\,\frac{\partial MSE}{\partial out_{O1}}=2\times \frac{1}{2}(Target_{out_{O1} }-out_{O1})^{2-1}\times -1+0 \\=-(0.01-0.75136507)=0.74136507$
$\frac{\partial out_{O1}}{\partial z_{O1}} \rightarrow out_{O1}=\frac{1}{1+e^{-z_{O1}}} \rightarrow \frac{\partial out_{O1}}{\partial z_{O1}}= \frac{e^{-z_{O1}}}{(1+e^{-z_{O1}})^{2}} =0.1868156018$
$\frac{\partial z_{O1}}{\partial w_{5}} \rightarrow z_{O1}=out_{N1}*w_{5}+out_{N2}*w_{6}+b_{1} \rightarrow \frac{\partial z_{O1}}{\partial w_{5}}=0.593269992$
We have calculated all partial derivatives. Now we can calculate the gradient of MSE with respect to $w_{5}$: $\frac{\partial MSE}{\partial w_{5}}$:
$\Large \frac{\partial MSE}{\partial w_{5}}= \frac{\partial MSE}{\partial out_{O1}}\times \frac{\partial out_{O1}}{\partial z_{O1}}\times \frac{\partial z_{O1}}{\partial w_{5}}$$=0.74136507\times 0.1868156018 \times 0.593269992=0.0821670401$
$\Large \frac{\partial MSE}{\partial w_{5}}$$=0.0821670401$
This partial derivatives of $MSE$ with respect to other weights $w_{1},w_{2},w_{3},w_{4},w_{6},w_{7},w_{8}$ and bias $b1_{N1},b1_{N2},b1_{O1},b1_{O2}$ can be calculated by using chain rule as we did.
The next step is to decrease the MSE by tuning $w_{5}$ using Gradient Descent:
$\large w_{5}^{u}=w_{5}-\alpha \frac{\partial MSE}{\partial w_{5}}$
If learning rate $\alpha$=0.5, then the updated weight $ w_{5}^{u}$ to decrease MSE is calculated as:
$\large w_{5}^{u}$$=0.4-0.5* 0.0821670401=0.35891648$
This process should be repeated for many iteration to optimize $w_{5}$. See lecture before for more information about Gradient Descent. The entire process should be applied to uptimize other weights $w_{1},w_{2},w_{3},w_{4},w_{6},w_{7},w_{8}, b1_{N1},b1_{N2},b1_{O1},b1_{O2}$.
Small Examples¶
We start to build a ANN using tensorflow library.
import tensorflow as tf
from tensorflow import keras
We want to build a neural network structure for a binary classification and regression. The network structure has 1 hidden layers with 6 neurons (see Figure below).
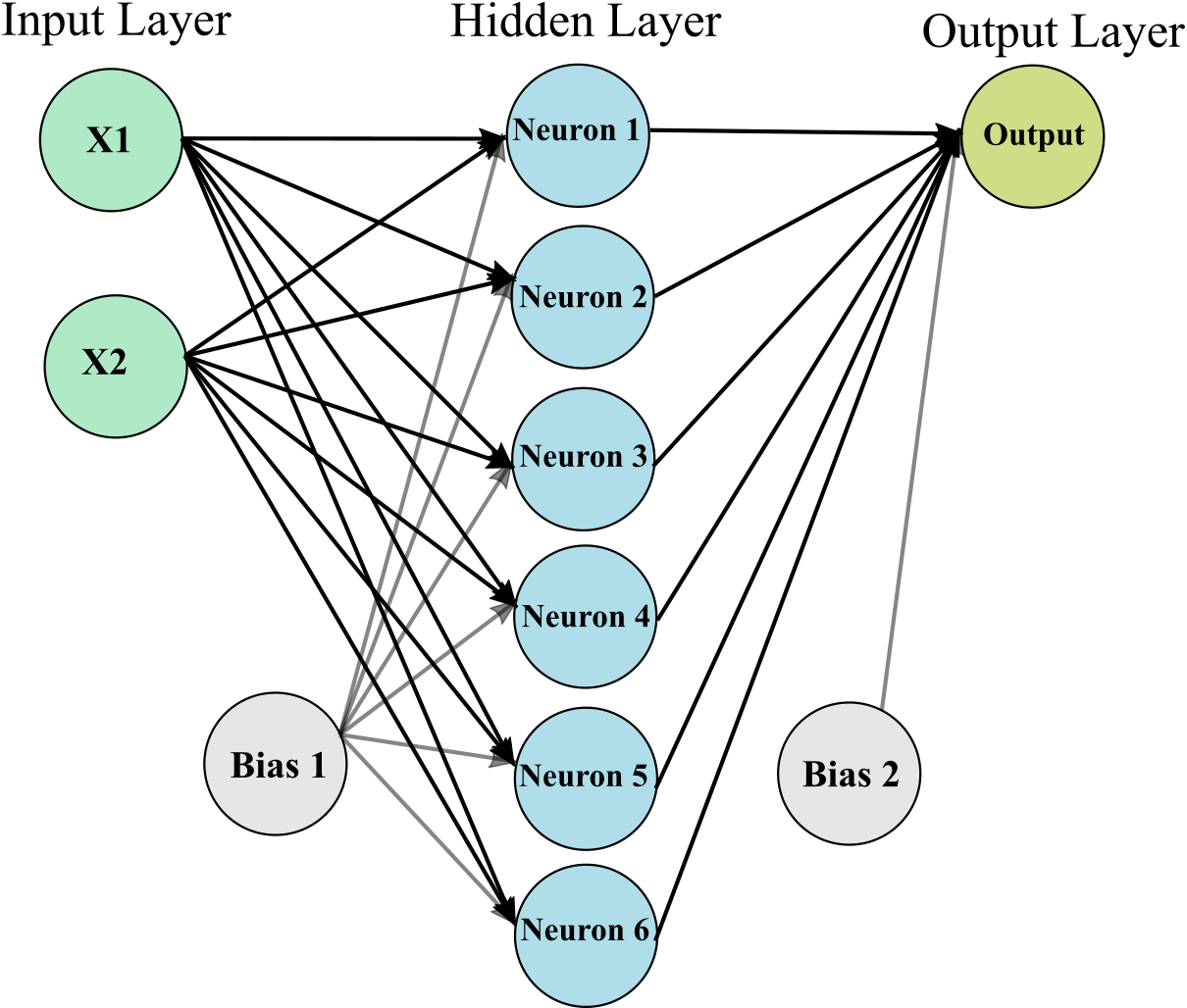
Classification (binary)¶
Here is a synthetic data set with two features and only 4 training instances.
X=[[1.5,2.2],
[-1.1,1.6],
[-2.7,-0.5],
[3.1,2.5]]
y=[1,
0,
0,
1]
np.random.seed(42)
tf.random.set_seed(42)
keras.backend.clear_session() # Clear the previous model
# create model
model = keras.models.Sequential()
# Input & Hidden Layer 1
model.add(keras.layers.Dense(6, input_dim=np.array(X).shape[1], activation='sigmoid'))
# Output Layer
model.add(keras.layers.Dense(1,activation='sigmoid'))
# use activation="softmax" for multicalss classification
# Compile model
model.compile(optimizer='sgd',loss="binary_crossentropy",metrics=['accuracy'])
# sgd is stochastic gradient descent
# loss="binary_crossentropy" is for binary classification
# use loss="sparse_categorical_crossentropy" for multiclass classification
history=model.fit(X,y,verbose=0,epochs=200)
model.summary()
i=1
weights_input = model.layers[i].get_weights()[0]
print('Weights: ',weights_input)
Bias = model.layers[i].get_weights()[1]
print('Bias:',Bias)
pred=model.predict(X)
pred
The predict function gives probability of each class. We can simply convert to integer:
pred=[1 if i >= 0.5 else 0 for i in pred]
pred
Regression¶
X=[[1.5,2.2],
[-1.1,1.6],
[-2.7,-0.5],
[3.1,2.5]]
y=[1.6,
0.4,
0.98,
1.3]
np.random.seed(42)
tf.random.set_seed(42)
keras.backend.clear_session() # Clear the previous model
# create model
model = keras.models.Sequential()
# Input & Hidden Layer 1
model.add(keras.layers.Dense(6, input_dim=np.array(X).shape[1], activation='relu'))
# Output Layer
model.add(keras.layers.Dense(1))
# Compile model
model.compile(optimizer='sgd',loss="mse")
history=model.fit(X,y,verbose=0,epochs=300)
pred=model.predict(X)
pred
You can see by increasing number of epochs, the model will greatly overfit training data. The easiest technique is to apply early stopping as we discussed before; it stops iteration when error in validation set start to increase while error in training set keep decreasing. So, first you need to divide data into training set and test set; then the training set should be divided to smaller training set and validation. The test set should be applied in the end only for measuring the error of the model.
Visit the TensorFlow Playground at https://playground.tensorflow.org/, play with the parameters, change Hidden layera, Neurons.. choose regression and classification task to understand the problem
Energy Efficiency Data Set¶
Lets apply ANN for Energy Efficiency data set for both regression and classification. First get training data:
Binary Classification¶
import pandas as pd
import numpy as np
from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
df = pd.read_csv('Building_Heating_Load.csv',na_values=['NA','?',' '])
np.random.seed(32)
df=df.reindex(np.random.permutation(df.index))
df.reset_index(inplace=True, drop=True)
#
df_binary=df.copy()
df_binary.drop(['Heating Load','Multi-Classes'], axis=1, inplace=True)
#
df_binary['Binary Classes']=df_binary['Binary Classes'].replace('Low Level', 0)
df_binary['Binary Classes']=df_binary['Binary Classes'].replace('High Level', 1)
# Training and Test
spt = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_idx, test_idx in spt.split(df_binary, df_binary['Binary Classes']):
train_set = df_binary.loc[train_idx]
test_set = df_binary.loc[test_idx]
#
X_train = train_set.drop("Binary Classes", axis=1)
y_train = train_set["Binary Classes"].values
#
scaler = StandardScaler()
X_train_Std=scaler.fit_transform(X_train)
# Smaller Training
# You need to divid your data to smaller training set and validation set for early stopping.
Training_c=np.concatenate((X_train_Std,np.array(y_train).reshape(-1,1)),axis=1)
Smaller_Training, Validation = train_test_split(Training_c, test_size=0.2, random_state=100)
#
Smaller_Training_Target=Smaller_Training[:,-1]
Smaller_Training=Smaller_Training[:,:-1]
#
Validation_Target=Validation[:,-1]
Validation=Validation[:,:-1]
Lets now train a ANN for binary classification with 3 hidden layers; each layer has 50 neurons. Th following code implement early stopping to avoid overfitting.
np.random.seed(42)
tf.random.set_seed(42)
keras.backend.clear_session() # Clear the previous model
# create model
model = keras.models.Sequential()
# Input & Hidden Layer 1
model.add(keras.layers.Dense(50, input_dim=np.array(Smaller_Training).shape[1], activation='relu'))
# Hidden Layer 2
model.add(keras.layers.Dense(50,activation='relu'))
# Hidden Layer 3
model.add(keras.layers.Dense(50,activation='relu'))
# Output Layer
model.add(keras.layers.Dense(1,activation='sigmoid'))
# use activation="softmax" for multicalss classification
# Compile model
model.compile(optimizer='adam',loss="binary_crossentropy",metrics=['accuracy'])
#'adam' is another optimization approach is more efficient than sgd. We will talk about it in more details.
# Early stopping to avoid overfitting
monitor= keras.callbacks.EarlyStopping(monitor='val_loss', min_delta=1e-3,patience=3, mode='auto')
history=model.fit(Smaller_Training,Smaller_Training_Target,batch_size=32,validation_data=
(Validation,Validation_Target),callbacks=[monitor],verbose=0,epochs=1000)
import matplotlib.pyplot as plt
def plot(history):
font = {'size' : 10}
plt.rc('font', **font)
fig, ax=plt.subplots(figsize=(12, 4), dpi= 110, facecolor='w', edgecolor='k')
ax1 = plt.subplot(1,2,1)
history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']
epochs = range(1, len(loss_values) + 1)
plt.plot(epochs, loss_values, 'bo', label='Training loss')
plt.plot(epochs, val_loss_values, 'r', label='Validation loss',linewidth=2)
plt.title('Training and Validation Loss',fontsize=14)
plt.xlabel('Epochs (Early Stopping)',fontsize=12)
plt.ylabel('Loss',fontsize=11)
plt.legend(fontsize='12')
# plt.ylim((0, 0.8))
ax2 = plt.subplot(1,2,2)
history_dict = history.history
loss_values = history_dict['accuracy']
val_loss_values = history_dict['val_accuracy']
epochs = range(1, len(loss_values) + 1)
ax2.plot(epochs, loss_values, 'ro', label='Training accuracy')
ax2.plot(epochs, val_loss_values, 'b', label='Validation accuracy',linewidth=2)
plt.title('Training and Validation Accuracy',fontsize=14)
plt.xlabel('Epochs (Early Stopping)',fontsize=12)
plt.ylabel('Accuracy',fontsize=12)
plt.legend(fontsize='12')
# plt.ylim((0.8, 0.99))
plt.show()
plot(history)
# Prediction using trained ANN for entire training
pred=model.predict(Smaller_Training[:5])
pred=[1 if i >= 0.5 else 0 for i in pred]
pred
# Actual values
Smaller_Training_Target[:5]
Lets apply the trained model on the for the entire training set:
from sklearn.metrics import accuracy_score
pred=model.predict(X_train_Std)
pred=[1 if i >= 0.5 else 0 for i in pred]
acr=accuracy_score(y_train, pred)
print(acr)
Lets apply the model on test set which is the data that model has never seen before.
X_test = test_set.drop("Binary Classes", axis=1)
y_test = test_set["Binary Classes"].values
#
X_test_Std=scaler.transform(X_test)
from sklearn.metrics import accuracy_score
pred=model.predict(X_test_Std)
pred=[1 if i >= 0.5 else 0 for i in pred]
acr=accuracy_score(y_test, pred)
print(acr)
Multiclass Classification¶
from sklearn.preprocessing import OrdinalEncoder
df_multi=df.copy()
df_multi.drop(['Binary Classes','Heating Load'], axis=1, inplace=True)
#
ordinal_encoder = OrdinalEncoder()
Multi_Classes_encoded = ordinal_encoder.fit_transform(df_multi[['Multi-Classes']])
df_multi['Multi-Classes']=Multi_Classes_encoded
# Training and Test
spt = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_idx, test_idx in spt.split(df_multi, df_multi['Multi-Classes']):
train_set = df_multi.loc[train_idx]
test_set = df_multi.loc[test_idx]
#
X_train = train_set.drop("Multi-Classes", axis=1)
y_train = train_set["Multi-Classes"].values
#
scaler = StandardScaler()
X_train_Std=scaler.fit_transform(X_train)
# Smaller Training
# You need to divid your data to smaller training set and validation set for early stopping.
Training_c=np.concatenate((X_train_Std,np.array(y_train).reshape(-1,1)),axis=1)
Smaller_Training, Validation = train_test_split(Training_c, test_size=0.2, random_state=100)
#
Smaller_Training_Target=Smaller_Training[:,-1]
Smaller_Training=Smaller_Training[:,:-1]
#
Validation_Target=Validation[:,-1]
Validation=Validation[:,:-1]
np.random.seed(42)
tf.random.set_seed(42)
keras.backend.clear_session() # Clear the previous model
# create model
model = keras.models.Sequential()
# Input and Hidden Layer 1
model.add(keras.layers.Dense(50, input_dim=np.array(Smaller_Training).shape[1], activation='relu'))
# Hidden Layer 2
model.add(keras.layers.Dense(50,activation='relu'))
# Hidden Layer 3
model.add(keras.layers.Dense(50,activation='relu'))
# Output Layer
model.add(keras.layers.Dense(4,activation='softmax'))
# we have 4 classes
# Compile model
model.compile(optimizer='adam',loss="sparse_categorical_crossentropy",metrics=['accuracy'])
#'adam' is another optimization approach is more efficient than sgd. We will talk about it in more details.
# Early stopping to avoid overfitting
monitor= keras.callbacks.EarlyStopping(monitor='val_loss', min_delta=1e-3,patience=3, mode='auto')
history=model.fit(Smaller_Training,Smaller_Training_Target,batch_size=32,validation_data=
(Validation,Validation_Target),callbacks=[monitor],verbose=0,epochs=1000)
plot(history)
# Prediction using trained ANN
pred=model.predict(Smaller_Training[:5])
pred=[np.argmax(prob) for prob in pred]
pred
# Actual values
Smaller_Training_Target[:5]
Apply the trained model for the entire training set:
pred=model.predict(X_train_Std)
pred=[np.argmax(prob) for prob in pred]
acr=accuracy_score(y_train, pred)
print(acr)
Lets apply the model on test set which is the data that model has never seen before.
X_test = test_set.drop("Multi-Classes", axis=1)
y_test = test_set["Multi-Classes"].values
#
X_test_Std=scaler.transform(X_test)
from sklearn.metrics import accuracy_score
pred=model.predict(X_test_Std)
pred=[np.argmax(prob) for prob in pred]
acr=accuracy_score(y_test, pred)
print(acr)
Regression¶
df_reg=df.copy()
df_reg.drop(['Binary Classes','Multi-Classes'], axis=1, inplace=True)
# Training and Test
train_set, test_set = train_test_split(df_reg, test_size=0.2, random_state=42)
#
X_train = train_set.drop("Heating Load", axis=1)
y_train = train_set["Heating Load"].values
#
scaler = StandardScaler()
X_train_Std=scaler.fit_transform(X_train)
# Smaller Training
# You need to divid your data to smaller training set and validation set for early stopping.
Training_c=np.concatenate((X_train_Std,np.array(y_train).reshape(-1,1)),axis=1)
Smaller_Training, Validation = train_test_split(Training_c, test_size=0.2, random_state=100)
#
Smaller_Training_Target=Smaller_Training[:,-1]
Smaller_Training=Smaller_Training[:,:-1]
#
Validation_Target=Validation[:,-1]
Validation=Validation[:,:-1]
np.random.seed(42)
tf.random.set_seed(42)
keras.backend.clear_session() # Clear the previous model
# create model
model = keras.models.Sequential()
# Input and Hidden Layer 1
model.add(keras.layers.Dense(50, input_dim=np.array(Smaller_Training).shape[1], activation='relu'))
# Hidden Layer 2
model.add(keras.layers.Dense(50,activation='relu'))
# Hidden Layer 3
model.add(keras.layers.Dense(50,activation='relu'))
# Output Layer
model.add(keras.layers.Dense(1))
# Compile model
model.compile(optimizer='adam',loss="mse")
# 'adam' is another optimization approach is more efficient than sgd. We will talk about it in more details.
# 'mse' is mean square error which is applied for regression
# Early stopping to avoid overfitting
monitor= keras.callbacks.EarlyStopping(monitor='val_loss', min_delta=1e-3,patience=3, mode='auto')
history=model.fit(Smaller_Training,Smaller_Training_Target,batch_size=32,validation_data=
(Validation,Validation_Target),callbacks=[monitor],verbose=0,epochs=1000)
def plot_NN(model,history,x_train,y_train):
""" Plot training loss versus validation loss and
training accuracy versus validation accuracy"""
font = {'size' : 7.5}
plt.rc('font', **font)
fig, ax=plt.subplots(figsize=(7, 5), dpi= 200, facecolor='w', edgecolor='k')
ax1 = plt.subplot(2,2,1)
history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']
epochs = range(1, len(loss_values) + 1)
ax1.plot(epochs, loss_values, 'bo',markersize=4, label='Training loss')
ax1.plot(epochs, val_loss_values, 'r-', label='Validation loss')
plt.title('Training and validation loss',fontsize=11)
plt.xlabel('Epochs (Early Stopping)',fontsize=9)
plt.ylabel('Loss',fontsize=10)
plt.legend(fontsize='8.5')
plt.ylim((0, 100))
ax2 = plt.subplot(2,2,2)
pred=model.predict(x_train)
t = pd.DataFrame({'pred': pred.flatten(), 'y': y_train.flatten()})
t.sort_values(by=['y'], inplace=True)
epochs = range(1, len(loss_values) + 1)
ax2.plot(t['pred'].tolist(), 'g', label='Prediction')
ax2.plot(t['y'].tolist(), 'm--o',markersize=2, label='Expected')
plt.title('Prediction vs Expected for Training',fontsize=11)
plt.xlabel('Data',fontsize=9)
plt.ylabel('Output',fontsize=10)
plt.legend(fontsize='8.5')
fig.tight_layout(w_pad=1.42)
plt.show()
plot_NN(model,history,Smaller_Training,Smaller_Training_Target)
Lets get RMSE for training set:
from sklearn.metrics import mean_squared_error
pred=model.predict(X_train_Std)
mse = mean_squared_error(y_train, pred)
rmse= np.sqrt(mse)
rmse
Get RMSE for test set:
X_test = test_set.drop("Heating Load", axis=1)
y_test = test_set["Heating Load"].values
#
X_test_Std=scaler.transform(X_test)
pred=model.predict(X_test_Std)
mse = mean_squared_error(y_test, pred)
rmse= np.sqrt(mse)
rmse
You should always expect less performance on test set since the model has not seen this data set before.
Fine-tune Neural Network Hyperparameters¶
Classification: GridSearchCV¶
You can use Scikit-Learn to fune-tune ANN's hyperparameters. You need a function for ANN to fine-tune hyperparameters. The following code is ANN with 3 hidden layers. You can adjust any hyperparameter.
def ANN (input_dim,neurons=50,loss="binary_crossentropy",activation="relu",Nout=1,
metrics=['accuracy'],activation_out='sigmoid'):
""" Function to run Neural Network for different hyperparameters"""
np.random.seed(42)
tf.random.set_seed(42)
# create model
model = keras.models.Sequential()
# Input and Hidden Layer 1
model.add(keras.layers.Dense(neurons,input_dim=input_dim, activation=activation))
# Input Layer 2
model.add(keras.layers.Dense(neurons,activation=activation))
# Input Layer 3
model.add(keras.layers.Dense(neurons,activation=activation))
# Output Layer
model.add(keras.layers.Dense(Nout,activation=activation_out))
# Compile model
model.compile(optimizer='adam',loss=loss,metrics=metrics)
return model
Then you can fine-tune number of neurons with the following code for the binary classification
# Training and Test
spt = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_idx, test_idx in spt.split(df_binary, df_binary['Binary Classes']):
train_set = df_binary.loc[train_idx]
test_set = df_binary.loc[test_idx]
#
X_train = train_set.drop("Binary Classes", axis=1)
y_train = train_set["Binary Classes"].values
#
scaler = StandardScaler()
X_train_Std=scaler.fit_transform(X_train)
# Smaller Training
# You need to divid your data to smaller training set and validation set for early stopping.
Training_c=np.concatenate((X_train_Std,np.array(y_train).reshape(-1,1)),axis=1)
Smaller_Training, Validation = train_test_split(Training_c, test_size=0.2, random_state=100)
#
Smaller_Training_Target=Smaller_Training[:,-1]
Smaller_Training=Smaller_Training[:,:-1]
#
Validation_Target=Validation[:,-1]
Validation=Validation[:,:-1]
The following code fine-tune only number of neuron, but you can simply apply for all parameters. The only issue is the process can be extremely computationally expensive and large number of parameters to adjust.
from keras.wrappers.scikit_learn import KerasClassifier
from sklearn.model_selection import GridSearchCV
# define the grid search parameters
param_grid = {'neurons' : [50,100,150]}
# Run Keras Classifier
model = KerasClassifier(build_fn=ANN,input_dim=Smaller_Training.shape[1])
# Apply Scikit Learn GridSearchCV
grid = GridSearchCV(estimator=model,param_grid=param_grid, cv=2)
# Early stopping to avoid overfitting
monitor= keras.callbacks.EarlyStopping(min_delta=1e-3,patience=5, verbose=0)
grid_result = grid.fit(Smaller_Training,Smaller_Training_Target,batch_size=32,validation_data=
(Validation,Validation_Target),callbacks=[monitor],
verbose=0,epochs=1000)
# Best result
print("Best parameters: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
You can fune-tune any ANN hyperparameter. Then call the function used fine-tuned neurons.
# Call Function with fined-tune numebr of neurons
model_ft=ANN (input_dim=Smaller_Training.shape[1],neurons=150)
# Early stopping to avoid overfitting
monitor= keras.callbacks.EarlyStopping(min_delta=1e-3,patience=5)
history=model_ft.fit(Smaller_Training,Smaller_Training_Target,batch_size=32,validation_data=
(Validation,Validation_Target),callbacks=[monitor],verbose=0,epochs=1000)
plot(history)
X_test = test_set.drop("Binary Classes", axis=1)
y_test = test_set["Binary Classes"].values
#
X_test_Std=scaler.transform(X_test)
from sklearn.metrics import accuracy_score
pred=model_ft.predict(X_test_Std)
pred=[1 if i >= 0.5 else 0 for i in pred]
acr=accuracy_score(y_test, pred)
print(acr)
You can see the accuracy you calculated is higher than "grid_result.bestscore" because of some overfiting. So, it is always a good idea
Regression: GridSearchCV¶
df_reg=df.copy()
df_reg.drop(['Binary Classes','Multi-Classes'], axis=1, inplace=True)
# Training and Test
train_set, test_set = train_test_split(df_reg, test_size=0.2, random_state=42)
X_train = train_set.drop("Heating Load", axis=1)
y_train = train_set["Heating Load"].values
#
scaler = StandardScaler()
X_train_Std=scaler.fit_transform(X_train)
# Smaller Training
# You need to divid your data to smaller training set and validation set for early stopping.
Training_c=np.concatenate((X_train_Std,np.array(y_train).reshape(-1,1)),axis=1)
Smaller_Training, Validation = train_test_split(Training_c, test_size=0.2, random_state=100)
#
Smaller_Training_Target=Smaller_Training[:,-1]
Smaller_Training=Smaller_Training[:,:-1]
#
Validation_Target=Validation[:,-1]
Validation=Validation[:,:-1]
from keras.wrappers.scikit_learn import KerasRegressor
# define the grid search parameters
param_grid = {'neurons' : [50,100,150]}
# Run Keras Classifier
model = KerasRegressor(build_fn=ANN,input_dim=Smaller_Training.shape[1],loss='mse'
,metrics=None,activation_out=None)
#model. _estimator_type = "regressor"
# Apply Scikit Learn GridSearchCV
grid = GridSearchCV(estimator=model,param_grid=param_grid, cv=2)
# Early stopping to avoid overfitting
monitor= keras.callbacks.EarlyStopping(min_delta=1e-3,patience=5, verbose=0)
grid_result = grid.fit(Smaller_Training,Smaller_Training_Target,batch_size=32,validation_data=
(Validation,Validation_Target),callbacks=[monitor],
verbose=0,epochs=1000)
# Best result
print("Best parameters: %f using %s" % (-1*grid_result.best_score_, grid_result.best_params_))
You can fune-tune any ANN hyperparameter. Then call the function used fine-tuned neurons.
# Call Function with fined-tune numebr of neurons
model_ft=ANN (input_dim=Smaller_Training.shape[1],neurons=150,loss='mse',metrics=None,activation_out=None)
# Early stopping to avoid overfitting
monitor= keras.callbacks.EarlyStopping(min_delta=1e-3,patience=5)
history=model_ft.fit(Smaller_Training,Smaller_Training_Target,batch_size=32,validation_data=
(Validation,Validation_Target),callbacks=[monitor],verbose=0,epochs=1000)
plot_NN(model_ft,history,Smaller_Training,Smaller_Training_Target)
X_test = test_set.drop("Heating Load", axis=1)
y_test = test_set["Heating Load"].values
#
X_test_Std=scaler.transform(X_test)
pred=model_ft.predict(X_test_Std)
mse = mean_squared_error(y_test, pred)
rmse= np.sqrt(mse)
rmse