Introduction
In this lecture, we will discuss an example of Machine Learning project from start to end. Assume that you recently hired as data scientist in a company. We will discuss what main steps you should go through to launch a Machine Learning project. We use the oil production dataset for 10000 hydrocarbon wells. The data file is WPD_10000.csv. The data is not original and manipulated so it should NOT be used for any other purposes than learning. The target is oil production prediction using well properties.
Big Picture¶
The first task you are asked as a data scientist is to build a model for oil prediction prediction using known information of hydrocarbon wells. Your model should learn from this data and be able to predict the oil production for those wells that oil production is unknown. See Figure below for location map of oil production $(10^{3}m^{3}/month)$ for 10000 hydrocarbon wells in Alberta.
import matplotlib
import pylab as plt
import numpy as np
import pandas as pd
font = {'size' : 6.5}
matplotlib.rc('font', **font)
fig = plt.subplots(figsize=(3.35,4.2), dpi= 200, facecolor='w', edgecolor='k')
df = pd.read_csv("WPD_10000.csv",na_values=['NA', '?','']) # Read data file
x=df['X Coordinate']; y=df['Y Coordinate']
var=df['OIL Prod. (e3m3/month)']
plt.scatter(x, y,c=var,s=(var)**(0.5),cmap='jet',edgecolors='k',linewidths=0.5,vmin=0, vmax=800)
plt.title('10000 Hydrocarbon Wells in Alberta' ,fontsize='8')
plt.xlabel('Easting (km)',fontsize='8'); plt.ylabel('Northing (km)',fontsize='8')
plt.colorbar(shrink=0.6,label='Oil Production (e3m3/month)',orientation='vertical')
Name=["" for x in range(6)]
Name[0:6]='Calgary','Fort McMurray','Edmonton','Rainbow',\
'Grande Prairie','Lloydminster'
xn=[365.3,557.2,426.8,91.8,84.3]
yn=[231.6,858.9,517.0,1087.2,713.4]
plt.plot(xn,yn,'*y',markersize=6,linewidth=1)
for i in range(5):
plt.text(xn[i], (yn[i]-18), Name[i],fontsize=5.2,color='y', fontweight='bold',style='oblique', ha='center',
va='top', wrap=True,bbox=dict(facecolor='k', alpha=1,pad=0))
plt.xlim((0, 650))
plt.ylim((0, 1200))
plt.show()
Problem Definition¶
Building a model is probably not the final goal. First, you should ask your boss what exactly is the business objective. How this model can be beneficial for the company? By answering these questions you define the problem, and decide what algorithms to use and how evaluate the performance of your model.
The next question is what the current solution looks like. This can give you a reference (baseline) performance, and insights on how to tackle the problem as well. Performance of your model should be higher than the reference performance. Your boss answers that the oil production are currently predicted manually by experts. The problem is this approach is very expensive and time-consuming, and their predictions are not great; when they can find out the actual oil production, they often realize that the estimates were off by more than 50%. That is the main reason why the company thinks that it would be useful to train a model to predict oil production given properties of wells.
Now you can start designing your system. First, you need to know: is it supervised, unsupervised? Obviously, this is a supervised learning task since you are given labeled training examples (each instance has the expected output which is oil production). Is it a classification task, a regression task, or something else? The answer is it is a typical regression task, since you are asked to predict a value; this is a multiple regression problem since the system will use multiple features (X Coordinate, Y Coordinate, Measured Depth (m)...) to make a prediction (OIL Prod.). It is also a univariate regression problem since a single value is predicted for each well. If we were trying to predict multiple values for each well, it would be a multivariate regression problem.
Performance Measurement¶
The next step is to select a performance measure. All the algorithms in machine learning rely on minimizing a function called cost and loss functions. A cost function is a measure of how bad the predictive model is to predict the actual outcome. We will talk about minimizing a cost function. A typical performance measurement (cost function) for regression problems is the Mean Square Error (MSE). See Equation below:
$MSE=\frac{1}{n}\sum_{i=1}^{n}(y_p^{i}-y_a^{i})^{2}$ where $y_p$ are $y_a$ predicted and actual values, respectively. See Figure below for an example of MSE.
font = {'size' : 12}
matplotlib.rc('font', **font)
fig = plt.subplots(figsize=(7, 5), dpi= 80, facecolor='w', edgecolor='k')
it=[];MSE=[]
no=0
for i in range(-50,50):
y_i=np.linspace(0.10+i/2.0,0.40+i/2.0,100) # Range of predicted values
y_a=np.linspace(0.20,0.30,100) # Range of actual values values
no+=1
it.append(no)
MSE.append(np.mean((y_i-y_a)**2))
plt.plot(it,MSE,linewidth=4)
plt.title('Mean Square Error (MSE) Cost Function' ,fontsize='16')
plt.xlabel('Number of Iteration',fontsize='14') ; plt.ylabel('MSE',fontsize='14')
plt.axis([1, 100, 0, 620])
plt.show()
MSE is usually preferred for performance measurement of most regression tasks. However, you may want to use another function to measure performance in some contexts. If you have a lot of outlier, you should consider Mean Absolute Error (MAE). MAE is the average of absolute differences between the predicted and actual values. See Equation below:
$MAE=\frac{1}{n}\sum_{i=1}^{n}\left | y_p^{i}-y_a^{i} \right |$ where $y_p$ are $y_a$ predicted and actual values, respectively. See Figure below for an example of MAE.
font = {'size' : 12}
matplotlib.rc('font', **font)
fig = plt.subplots(figsize=(7, 5), dpi= 80, facecolor='w', edgecolor='k')
it=[];MAE=[]
no=0
for i in range(-50,50):
y_i=np.linspace(0.10+i/2.0,0.40+i/2.0,100) # Range of predicted values
y_a=np.linspace(0.20,0.30,100) # Range of actual values values
no+=1
it.append(no)
MAE.append(np.mean(abs(y_i-y_a)))
plt.plot(it,MAE,linewidth=4)
plt.title('Mean Absolute Error (MAE) Cost Function' ,fontsize='16')
plt.xlabel('Number of Iteration',fontsize='14') ; plt.ylabel('MAE',fontsize='14')
plt.axis([1, 100, 0, 25])
plt.show()
Although the squared error is easier to solve, using the absolute error is more robust to outliers. The goal of machine learning model is to find the point that minimizes cost function. Both functions reach the minimum when the prediction is very close to the actual value. Since MSE squares the error ($E=(y_p-y_a)^{2}$), the value of error ($E$) increases a lot if $E$ > 1. If there is an outlier in data set, $E^{2}$ >> $|E|$. This model with MSE cost function gives more weight to outliers than a model with MAE loss. MAE is useful if the training data is corrupted with outliers: for example, erroneously receiving unrealistically large negative/positive values in training data, but not in testing data. If the outliers are important for business and should be detected, then MSE should be used. The predictions using MSE loss function get skewed towards outliers while MAE go towards median value.
Get the Data and Preprocessing¶
It is time to look at your data to gain some insights. You will need to install a number of Python modules discussed before: Pandas, Jupyter, NumPy, Pandas, Matplotlib, Scikit-Learn..
Shuffling and Look at the Data Structure
The first step after reading data in Python is to Shuffle data set to avoid any element of bias/patterns as discussed before.
import pandas as pd
from numpy import random
df= pd.read_csv("WPD_10000.csv",na_values=['NA', '?','']) # Read data file
np.random.seed(42)
Oil_Prod = df.reindex(np.random.permutation(df.index))
Oil_Prod.reset_index(inplace=True, drop=True) # Reset index
Oil_Prod[0:5] # Display top five rows
info() method is efficient to get a quick description of the data, number of rows, and type of each attribute and number of non-null values.
Oil_Prod.info()
The describe() function is used to present a summary of the numerical attributes. The null values are ignored. P25% is 25th percentile (or 1st quartile), P50% is the median, and P75% is 75th percentile (or 3rd quartile).
Oil_Prod.describe()
Another quick way to get a feel of the type of data is to plot a histogram for each numerical attribute. A histogram shows the number of instances (on the vertical axis) that have a given value range (on the horizontal axis). You can either plot this one attribute at a time, or you can call the hist() method on the whole dataset, and it will plot a histogram for each numerical attribute. See histograms of some features below:
columns=['X Coordinate','Y Coordinate','Measured Depth (m)','Surface-Casing Weight (kg/m)',
'Production-Casing Size (mm)','Bore. Temp. (degC)','Porosity (fraction)',
'Permeability (darcy)','OIL Prod. (e3m3/month)']
Oil_Prod[columns].hist(bins=15, layout=(3, 3), figsize=(15,10))
plt.show()
You can make a much nicer histogram by the code below:
def histplt (val,bins,title,xlabl,xlimt,axt=None):
""" Function for histogram plotting"""
from matplotlib.offsetbox import AnchoredText
ax1 = axt or plt.axes()
val=np.array(val)
plt.hist(val, bins=bins,ec='black')
n=len(val)
Mean=np.mean(val)
SD=np.sqrt(np.var(val))
Max=np.amax(val)
Min=np.amin(val)
txt='n=%.0f \n $\mu$=%.1f \n $\sigma$=%.1f \n Max=%.1f \n Min=%.1f'
anchored_text = AnchoredText(txt %(n,Mean,SD,Max,Min), loc=1)
ax1.add_artist(anchored_text)
plt.title(title,fontsize=font['size']*1.25)
plt.xlabel(xlabl,fontsize=font['size'])
plt.ylabel('Frequency',fontsize=font['size'])
plt.xlim(xlimt)
ax1.grid(linewidth='0.35')
font = {'size' : 10}
matplotlib.rc('font', **font)
fig = plt.subplots(figsize=(10, 3), dpi= 150, facecolor='w', edgecolor='k')
ax1=plt.subplot(1,2,1)
val=Oil_Prod['OIL Prod. (e3m3/month)']
histplt(val,bins=100,title='Histogram of Oil Production',xlabl='OIL Prod. (e3m3/month)',xlimt=(0,200),axt=ax1)
ax2=plt.subplot(1,2,2)
val=Oil_Prod['Measured Depth (m)']
histplt(val,bins=30,title='Histogram of Measured Depth',xlabl='Measured Depth (m)',xlimt=(0,4000),axt=ax2)
Remove Outliers¶
We discussed in previous lecture that outliers are usually extreme high or low values that are different from pattern of majority data. A straightforward approach to detect outliers are several (n) standard deviations from the mean $m\pm n\sigma$ ($m$=mean, $\sigma$=standard deviation). For example, an outlier can be bigger than $m+ 3\sigma $ or less than $m- 3\sigma $. The following function can be used to apply this approach.
def outlier_remove(df, n,name):
"""Delete rows for a specified column where values are out of +/- n*sd standard deviations
df : Pandas dataframe
n : n in the equation 𝑚±𝑛𝜎
name: Column name
"""
mean=df[name].mean() # Calclute mean of column
sd=df[name].std() # Calclute standard deviation of column
drop_r = df.index[(mean -n * sd> df[name]) | (mean+n * sd< df[name])]
df.drop(drop_r, axis=0, inplace=True)
df.reset_index(inplace=True, drop=True) # Reset index
# Drop outliers in last column 'OIL Prod. (e3m3/month)'
outlier_remove(Oil_Prod, n=3,name='OIL Prod. (e3m3/month)')
Oil_Prod.describe()
You should separate the attributes (features or predictors) and targets (labels) since you should not apply the same transformation to the predictors and the target values:
Set Aside Test Set¶
At this step you should set aside part of data as test set. and you should not look at test set until the end of project for only final evaluation of your predictive model. It might seem a little strange to voluntarily take some part of your data and not even have a glance. But your brain is an amazing pattern detection: if you look at the test set, you may come across interesting patterns in the test data that persuade you to choose a particular Machine Learning model. This leads to a very optimistic estimate, your model cannot generalize well. This is called data Snooping Bias. It is quite simple to theoretically create a test set, typically 20% of the dataset (Aurélien Géron, 2019).
There are different approaches to take some instances. We discussed how to use Pandas to do this. However, Scikit-Learn provides functions to split datasets into multiple subsets in various ways. The simplest function is train_test_split. If you do not want your data split changes for each run, you should set the random generator seed.
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(Oil_Prod, test_size=0.2, random_state=100)
This is a purely random sampling. If you have a very large dataset, this approach should be totally fine. However, if not, you may face a significant sampling bias. For example when a survey company wants to contact 1000 people, they do not randomly call 1000 people; they do their best to ensure 10000 people are representative of the whole population (Aurélien Géron, 2019); if the population of a city has 52% female and 48% male citizen, a reliable survey should preserve this ratio in sampling. This is called stratified sampling. If purely random sampling was used, the survey results would be significantly biased.
For a classification task, you should split your data in a way of having the same number of data for each class. For example, if you have two classes in your target: class 1 has 630 instances and class 2 has 370 instances, then you should set aside test set to have the same number of classes. If you are dealing with a regression task, you may divide your target into a few categories and then split the data to respect the number of instances for each category. The code below divide "OIL Prod_cat" to 4 categories. To limit number of categories, "OIL Prod. (e3m3/month)" is divided by 20 and rounding up using Ceil.
Oil_Prod["OIL Prod_cat"]=np.ceil(Oil_Prod["OIL Prod. (e3m3/month)"] / 20)
Oil_Prod["OIL Prod_cat"].where(Oil_Prod["OIL Prod_cat"] < 4, 4, inplace=True)
Oil_Prod[0:4]
# Plot histogram of categories
font = {'size' : 14}
matplotlib.rc('font', **font)
histplt(Oil_Prod["OIL Prod_cat"],bins=15,title='Number of Instances per Class ',xlabl='Categories',
xlimt=(0.68,4.3),axt=ax1)
Now you can do stratified sampling based on the "OIL Prod_cat" category. you can use Scikit-Learn’s StratifiedShuffleSplit function:
from sklearn.model_selection import StratifiedShuffleSplit
spt = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=100)
for train_idx, test_idx in spt.split(Oil_Prod, Oil_Prod["OIL Prod_cat"]):
train_set_strat = Oil_Prod.loc[train_idx]
test_set_strat = Oil_Prod.loc[test_idx]
test_set_strat[0:4]
# Plot histogram of test set for categories
font = {'size' : 14}
matplotlib.rc('font', **font)
histplt(test_set_strat["OIL Prod_cat"],bins=15,title='Test_Number of Instances',
xlabl='Categories',xlimt=(0.68,4.3),axt=ax1)
Now you should remove the OIL Prod_cat attribute in order to retrieve the original state of data.
for dataset in (train_set_strat, test_set_strat):
dataset.drop("OIL Prod_cat", axis=1, inplace=True)
dataset.reset_index(inplace=True, drop=True) # Reset index
train_set_strat[0:4]
It is often ignored to set aside some data as test set. However, this is a critical step for Machine Learning project since we may end up a very optimistic predictive model. Now we should move on to the stage of exploring the data.
Visualize the Data¶
We have only taken a quick look at the data. Now we should go deeper in data visualization. At this step, we should make sure to work only on the training set and do not touch the test set achieved in the last section. If the training set is very large, you may sample an exploration set to make a very fast and easy manipulations. This data set is small that we can work directly on the full set. It is a good idea to have a copy of your training set to avoid modifying the original data.
Oil_Prod = train_set_strat.copy()
Oil_Prod.describe()
Location Map¶
Due to having "X Coordinate" and "Y Coordinate", it is a good idea to have a location map of oil production to visualize the data.
# Change alpha for a better visualization and highlighting high-density areas
Oil_Prod.plot(kind="scatter", x="X Coordinate", y="Y Coordinate",fontsize=14,figsize=(7,9),alpha=0.15)
plt.xlabel('X Coordinate',fontsize=14)
plt.ylabel('Y Coordinate',fontsize=14)
plt.show()
You can make a nicer location map using matplotlib:
font = {'size' : 6.5}
matplotlib.rc('font', **font)
fig = plt.subplots(figsize=(3.35,4.2), dpi= 200, facecolor='w', edgecolor='k')
x=Oil_Prod['X Coordinate']; y=Oil_Prod['Y Coordinate']
var=Oil_Prod['OIL Prod. (e3m3/month)']
plt.scatter(x, y,c=var,s=(var)**(0.55),cmap='jet',edgecolors='k',linewidths=0.5,vmin=0, vmax=400)
plt.title('Training set: '+str(len(var))+' Hydrocarbon Wells in Alberta' ,fontsize='7')
plt.xlabel('Easting (km)',fontsize='7'); plt.ylabel('Northing (km)',fontsize='7')
plt.colorbar(shrink=0.6,label='Oil Production (e3m3/month)',orientation='vertical')
Name=["" for x in range(6)]
Name[0:6]='Calgary','Fort McMurray','Edmonton','Rainbow',\
'Grande Prairie','Lloydminster'
xn=[365.3,557.2,426.8,91.8,84.3]
yn=[231.6,858.9,517.0,1087.2,713.4]
plt.plot(xn,yn,'*y',markersize=6,linewidth=1)
for i in range(5):
plt.text(xn[i], (yn[i]-18), Name[i],fontsize=5.2,color='y', fontweight='bold',style='oblique', ha='center',
va='top', wrap=True,bbox=dict(facecolor='k', alpha=1,pad=0))
plt.xlim((0, 650))
plt.ylim((0, 1200))
plt.show()
Calculate Correlations¶
You can compute the standard covariance between variables called correlation coefficient (Pearson’s r) between every pair of attributes. The correlation coefficient $\large \rho_{XY}$ is between -1 and +1.
$\large \rho_{XY}=\frac{C_{XY}}{\sqrt{\sigma_{X}^{2}\sigma_{Y}^{2}}}$ where $C_{XY}$ is the covariance between $XY$ and $\sigma_{X}^{2}$ and $\sigma_{Y}^{2}$ are variances for X and Y variables. The covariance is the variance between two variable. See Variance for more information.
$\large m_{X}=\frac{1}{n}\sum_{i=1}^{n}X_{i}\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\, \sigma_{X} ^{2}=\frac{1}{n}\sum_{i=1}^{n}\left ( X_{i}-m_{X} \right )^2\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\, C_{XY}=\frac{1}{n}\sum_{i=1}^{n}\left ( X_{i}-m_{X} \right )\left ( Y_{i}-m_{Y} \right )$
where $m_{X}$ is the mean of $X$ and $m_{Y}$ is the mean of $Y$. If absolute value of $ \rho_{XY}$ is close to 1 ($ \rho_{XY}$ ≈ −1 𝑜𝑟 1), it implies that two variables are perfectly correlated. If the $ \rho_{XY}$ is close to zero ($\rho_{XY}$ ≈ 0), two variables may be independent. However, $\rho_{XY}$ ≈ 0 does not necessarily imply independence between the two variables. See Figure below for various plots of correlation coefficients between their horizontal and vertical axes.
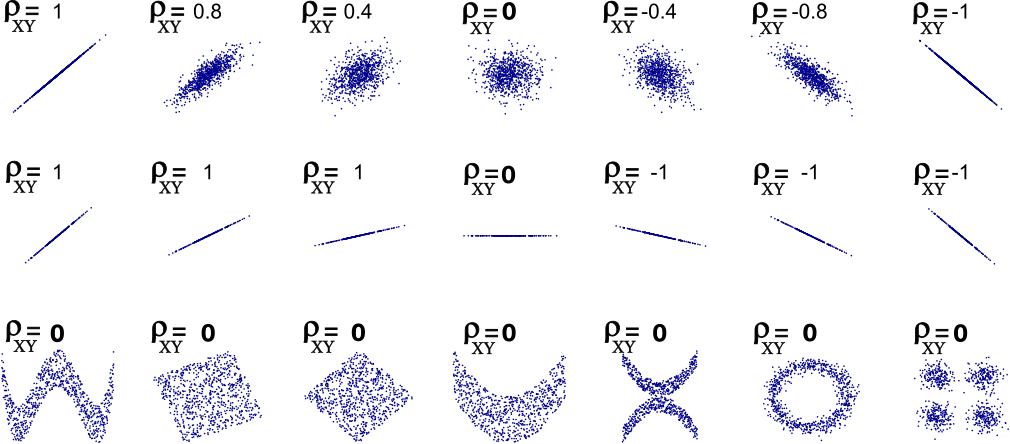
Image retrieved from Wikipedia.
As you can see, the correlation coefficient only measures linear correlations. For example if X increases, Y generally goes up and vice versa. All the plots of the bottom row have $\rho_{XY}=0$ although they are not obviously independent: they have non-linear relationships.
corr() function calculates correlation coefficient between variables. First we need to convert text number. We will discuss this in more details.
Oil_Prod['Deviation (True/False)']=Oil_Prod['Deviation (True/False)'].replace('False.', 0) # Replace False with 0
Oil_Prod['Deviation (True/False)']=Oil_Prod['Deviation (True/False)'].replace('True.', 1) # Replace True with 1
#
Oil_Prod['Prod. Formation']=Oil_Prod['Prod. Formation'].replace('Sand', 0) # Replace Sand with 0
Oil_Prod['Prod. Formation']=Oil_Prod['Prod. Formation'].replace('Shale-Sand', 1) # Replace Shale-Sand with 1
Oil_Prod['Prod. Formation']=Oil_Prod['Prod. Formation'].replace('Shale', 2) # Shale True with 2
Oil_Prod
corr_matrix=Oil_Prod.corr()
corr_matrix
# sort correlation of attributes with respect to target "OIL Prod. (e3m3/month)"
corr_matrix["OIL Prod. (e3m3/month)"].sort_values(ascending=False)
There is a very high correlation for porosity and permeability. You can make a nice plot as correlation bar using the function below:
def corr_bar(df):
"""Plot correlation bar with the pair of atrribute with last column"""
corr=df.corr()
Colms_sh=list(list(corr.columns))
coefs=corr.values[:,-1][:-1]
names=Colms_sh[:-1]
r_ = pd.DataFrame( { 'coef': coefs, 'positive': coefs>=0 }, index = names )
r_ = r_.sort_values(by=['coef'])
r_['coef'].plot(kind='barh', color=r_['positive'].map({True: 'b', False: 'r'}))
plt.xlabel('Correlation Coefficient',fontsize=6)
plt.vlines(x=0,ymin=-0.5, ymax=10, color = 'k',linewidth=0.8,linestyle="dashed")
plt.show()
font = {'size' : 5}
matplotlib.rc('font', **font)
ax1 = plt.subplots(figsize=(2.8, 3), dpi= 200, facecolor='w', edgecolor='k')
# Plot correlations of attributes with the last column
corr_bar(Oil_Prod)
font = {'size' : 10}
matplotlib.rc('font', **font)
from pandas.plotting import scatter_matrix
scatter_matrix(Oil_Prod[columns[0:3]],figsize=(12, 8),alpha=0.1)
plt.show()
You can make a nicer crossplot using matplotlib:
def CrossPlot (x,y,xlabl,ylabl,axt=None):
'''Cross plot between two variables'''
from matplotlib.offsetbox import AnchoredText
ax1 = axt or plt.axes()
x=np.array(x)
y=np.array(y)
n_x=len(x)
Mean_x=np.mean(x)
SD_x=np.sqrt(np.var(x))
n_y=len(y)
Mean_y=np.mean(y)
SD_y=np.sqrt(np.var(y))
corr=np.corrcoef(x,y)
plt.plot(x,y,'ro',markersize=2,alpha=0.08)
txt='$\\rho_{XY}$=%.3f \n $n$=%.0f \n $\mu_{X}$=%.1f \n $\sigma_{X}$=%.1f \n '
txt+=' $\mu_{Y}$=%.1f \n $\sigma_{Y}$=%.1f'
anchored_text = AnchoredText(txt %(corr[1,0], n_x,Mean_x,SD_x,Mean_y,SD_y), loc=1)
ax1.add_artist(anchored_text)
plt.xlabel(xlabl,fontsize=font['size'])
plt.ylabel(ylabl,fontsize=font['size'])
font = {'size' :7 }
matplotlib.rc('font', **font)
fig=plt.figure(figsize=(8, 2.65), dpi= 120, facecolor='w', edgecolor='k')
ax1 = plt.subplot(1,2,1)
CrossPlot (x=Oil_Prod['X Coordinate'],y=Oil_Prod['Measured Depth (m)'],xlabl='X Coordinate',
ylabl='Measured Depth (m)',axt=ax1)
ax2 = plt.subplot(1,2,2)
CrossPlot (x=Oil_Prod['Porosity (fraction)'],y=Oil_Prod['Permeability (darcy)'],xlabl='Porosity',
ylabl='Permeability',axt=ax2)
Data Preparation for Machine Learning Algorithms¶
After looking at the data, it’s time to prepare the data for your Machine Learning algorithms. You need to automate this preparation by writing some functions (instead of doing manually) because of several reasons:
Apply the transformations easily on any dataset (for example a new dataset).
Build a library of transformation functions for future projects.
# Note that drop() creates a copy and does not affect train_set_strat
Oil_Prod = train_set_strat.drop("OIL Prod. (e3m3/month)", axis=1)
Oil_Prod_Target = train_set_strat["OIL Prod. (e3m3/month)"].copy()
Imputation¶
Most Machine Learning algorithms cannot work with missing values, so a few functions should be written to take care of them. For example the attributes "Surface-Casing Weight (kg/m)", "Production-Casing Size (mm)", "Production-Casing Weight (kg/m)", "Bore. Temp. (degC)" have a lot of missing value. As we talked in previous lectures, you have three options to take care of missing values: 1- Get rid of the whole attributes (not recommended), 2- Rows that have missing values (may not be efficient, 3- Recommended to impute missing values with statistical value retrieved from the attribute (the median, the mean, etc.). We discussed how to do these with Pandas in previous lectures. Here, we apply Scikit-Learn to do this which is much easier. First, create a SimpleImputer instance, specifying that attribute’s missing values are imputed with the median of that attribute:
from sklearn.impute import SimpleImputer
imput_mdn = SimpleImputer(strategy="median")
Imputation may only be applied for numerical attributes, so need to have a copy of the data without the text attribute including "Deviation (True/False)" and "Prod. Formation":
Oil_Prod_num = Oil_Prod.drop(["Deviation (True/False)","Prod. Formation"], axis=1)
Oil_Prod_num[0:10]
Now you can calculate the median of each attribute by fitting imputer to the training data using the fit() method. The results are stored in its statistics_
imput_mdn.fit(Oil_Prod_num)
imput_mdn.statistics_
We trained an imputer; this “trained” imputer can be applied to transform the training set: missing values of each attribute can be replaced by the learned medians.
im = imput_mdn.transform(Oil_Prod_num)
The result of imputation is a NumPy array for each feature. We need to put it back into a Pandas DataFrame:
Oil_Prod_im = pd.DataFrame(im, columns=Oil_Prod_num.columns)
Oil_Prod_im
Deal with Text and Categorical Attributes¶
Most Machine Learning algorithms work with numbers anyway, so all texts and categorical variables should be efficiently converted to numbers before feeding Machine learning algorithms. For example "Deviation (True/False)" and "Prod. Formation" have texts. We discussed how to do this with Pandas in previous lectures. Here, we apply Scikit-Learn library.
Categorical Feature 1 (Prod. Formation)
Oil_Prod_cat = Oil_Prod[["Prod. Formation"]]
Oil_Prod_cat[0:10]
Oil_Prod['Prod. Formation'].value_counts()
gb_mean=df.groupby('Prod. Formation')['OIL Prod. (e3m3/month)'].mean()
gb_mean
from sklearn.preprocessing import OrdinalEncoder
ordinal_encoder = OrdinalEncoder()
Oil_Prod_cat_encoded = ordinal_encoder.fit_transform(Oil_Prod_cat)
Oil_Prod_cat_encoded[:10]
A number from 0 to 2 is assigned to each category: Sand=0, Shale=1 and Shale-Sand=2. One challenge with this approach is that Machine Learning algorithms assume that two nearby (for example 0 and 1) values are more similar than two distant values (0 to 2): for example, categories such as “Bad”, “Average”, “Good”, “Excellent”). However, this may not be correct for all cases. To fix this issue as it was discussed before, one binary attribute per category is created: one attribute equal to 1 when the category is Sand (and 0 otherwise), another attribute equal to 1 when the category is Shale (and 0 otherwise), and finally attribute equal to 1 when the category is Shale-Sand (and 0 otherwise). This process should be applied for all categories. This is called one-hot encoding, because only one attribute will be equal to 1 (hot), while the others will be 0 (cold). The new attributes are sometimes called dummy attributes. Scikit-Learn provides a function to convert categorical values into one-hot vectors (Aurélien Géron, 2019).
from sklearn.preprocessing import OneHotEncoder
cat_encoder = OneHotEncoder()
Oil_Prod_cat_1hot = cat_encoder.fit_transform(Oil_Prod_cat)
Oil_Prod_cat_1hot
Instead of a NumPy array, the output is a SciPy sparse matrix which is useful When dealing with many categories. The matrix is full of zeros except for a single 1 per row. It would be very wasteful to use tons of memory to store zeros instead a sparse matrix can stores only non‐zero elements. You can can convert a sparse matrixit to a NumPy array by toarray() function.
cat_hot_toarray_1=Oil_Prod_cat_1hot.toarray()
cat_hot_toarray_1[0:10]
You can see the list of categories:
cat_encoder.categories_
Categorical Feature 2 (Deviation (True/False))
We have another categorical variable "Deviation (True/False)"; the same approach should be applied.
Oil_Prod_cat = Oil_Prod[["Deviation (True/False)"]]
Oil_Prod_cat[0:10]
Oil_Prod_cat_2hot = cat_encoder.fit_transform(Oil_Prod_cat)
cat_hot_toarray_2=Oil_Prod_cat_2hot.toarray()
cat_hot_toarray_2[0:10]
cat_encoder.categories_
Scale Feature Values¶
If the input attributes have very different scales, Machine Learning algorithms don’t perform well; so it is very important to transform the data and make them all scale consistent. We applied imputed data from Imputation Section. Let's look at the range of data for each attribute again:
Oil_Prod_im.describe()
Standardization and min-max scaling are two common approaches to get all attributes to have the same scale. Min-max scaling is simply shifting and rescaling data value to be in range of 0 to 1. This can be done by subtracting the min value to have a shifted values and then dividing by the max of shifted values. See simple example below:
# Simple example for Min-max scaling
X=[1800,48,6,910,90,47,45]
X_shift=[i-min(X) for i in X]
X_MinMax=[i/max(X_shift) for i in X_shift]
X_MinMax
Scikit-Learn has a transformer called MinMaxScaler for Min-max scaling. See the code below how to do min-max scaling for all features with Scikit-Learn.
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
Oil_Prod_im_MMS=Oil_Prod_im.copy()
scaler.fit_transform(Oil_Prod_im_MMS)
As it was discussed before, standardization is different: the data values should be first subtracted the mean value; this leads to mean=0, and then the data are divided by the standard deviation so that the standardized values have variance 1; standardization does not force values to a specific range (unlike min-max scaling,). This might be problematic for some algorithms. However, standardization is much less affected by outliers. See the code below as a simple example:
# Simple example for StandardScaler
X=[1800,48,6,910,90,47,45]
X_shift=[i-np.mean(X) for i in X]
X_Standardiation=[i/np.sqrt(np.var(X_shift)) for i in X_shift]
X_Standardiation
For standardization, Scikit-Learn has a transformer called StandardScaler. See the code below for standardization of all features:
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
Oil_Prod_im_MMS=Oil_Prod_im.copy()
Oil_Prod_im_Std=scaler.fit_transform(Oil_Prod_im_MMS)
Oil_Prod_im_Std
As with all the transformations, it is important to fit the scalers to the training data only, not to the full dataset.
Concatenate Scaled and One-hot Encoded Feature¶
We applied imputation to predict the missing values (Oil_Prod_im) and then applied standardization for imputed data (Oil_Prod_im_Std). We also converted two categorical variable ("Prod. Formation" and "Deviation (True/False)") to numbers using one-hot encoding (cat_hot_toarray_1, cat_hot_toarray_2). Now, these variables should be concatenated using Numpy concatenate() function to use as training set.
Oil_Prod_prepared=np.concatenate((Oil_Prod_im_Std,cat_hot_toarray_1, cat_hot_toarray_2), axis=1)
Oil_Prod_prepared[0:4]
Model Training and Evaluation¶
Finally, you defined the problem, explored data and divided into training set and test set, and you applied transformation to feed Machine Learning algorithms more reliable data. Now you are ready to choose and train a Machine Learning algorithms. Let's train a very simple Linear Regression Model using Scikit-Learn.
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(Oil_Prod_prepared, Oil_Prod_Target)
some_data_prepared=Oil_Prod_prepared[-5:]
some_data_Target=Oil_Prod_Target[-5:]
print("Predictioned Oil Production (e3m3/month) \n:", lin_reg.predict(some_data_prepared))
print("Actuals Oil Production (e3m3/month): \n", list(some_data_Target))
The predictions are not accurate. We can calculate Root Mean Square Error (RMSE) between the predicted and actual values for the entire training set using Scikit-Learn’s mean_squared_error function:
from sklearn.metrics import mean_squared_error
Oil_Prod_predictions = lin_reg.predict(Oil_Prod_prepared)
mse_lin = mean_squared_error(Oil_Prod_Target, Oil_Prod_predictions)
rmse_lin= np.sqrt(mse_lin)
rmse_lin
This prediction is better than nothing; however, it should not be a great score: most oil production ("OIL Prod. (e3m3/month") values are between 11 to 89 (P25% to P75%) so a prediction error of 35 may not be efficient. This is a case of underfitting since the model is not powerful enough to make a good prediction. To resolve underfitting, you can choose a more powerful model, or select better features to feed Machine Learning algorithms, or to reduce the constraints on the model (this is not the case here sine we have not applied any constraints). You could try to add more features for example a well has many properties that can have an impact for oil production. But what if we try a more complex model.
We can apply a regression model of Decision Tree technique (Decision Trees will be discussed in more detail in next lectures). Decision Trees is one of powerful models for finding complex nonlinear relationships in the data.
from sklearn.tree import DecisionTreeRegressor
dtree_reg = DecisionTreeRegressor(random_state=40)
dtree_reg.fit(Oil_Prod_prepared, Oil_Prod_Target)
some_data_prepared=Oil_Prod_prepared[-5:]
some_data_Target=Oil_Prod_Target[-5:]
print("Predictioned Oil Production (e3m3/month): \n", dtree_reg.predict(some_data_prepared))
print("Actuals Oil Production (e3m3/month): \n", list(some_data_Target))
Oil_Prod_predictions = dtree_reg.predict(Oil_Prod_prepared)
tree_mse = mean_squared_error(Oil_Prod_Target, Oil_Prod_predictions)
tree_rmse = np.round(np.sqrt(tree_mse),5)
tree_rmse
Wow! This is an amazing model. Zero error! it perfectly predicted all training instances! But wait, this may be a clear example of very bad overfitting the training data. How can we make sure that it is overfitting? As we discussed before, the test set should be untouched until a reliable model is achieved. What you can do to void overfitting or underfitting?
Divide the Training Data to Smaller Training and Validation Sets¶
You can assign part of the training data for a smaller training set and a validation set. See Figure below. You should train your model with the smaller training set and validate it with validation. This process should be repeated until you achieve a satisfying model that neither overfitting nor underfitting. Finally you should only test your satisfied model to quantify the error of your model for never-before-seen dataset. That is it. Avoid temptation to tune your model again to have better performance on test set.
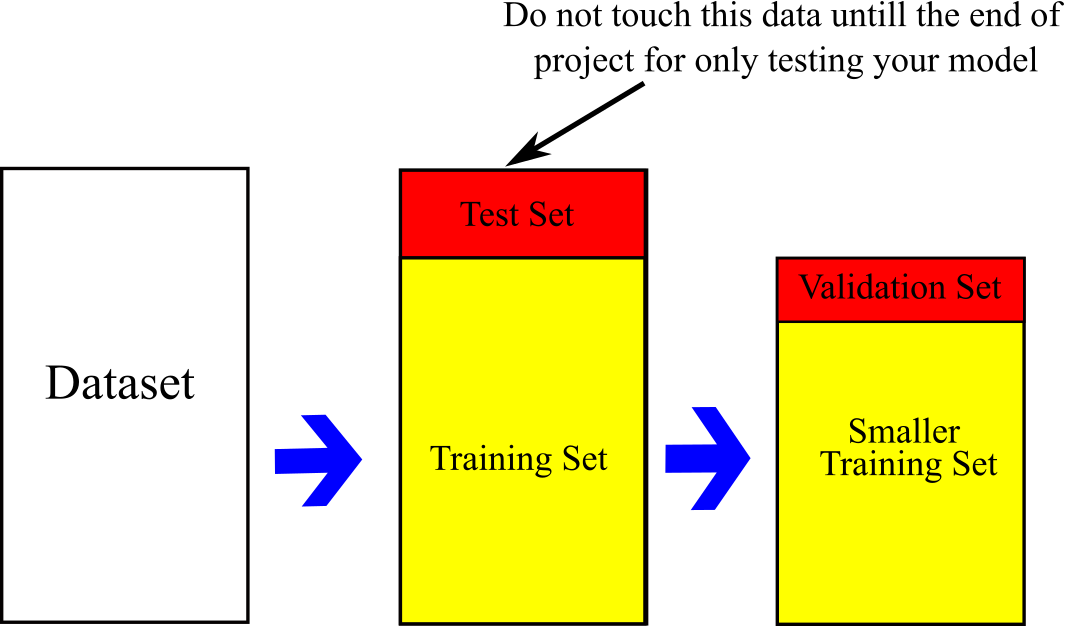
You can use again Scikit-Learn train_test_split function to split the training set into a smaller training set and a validation set. But first you need to convert the prepared data format into Pandas DataFrame:
Feature_list=['Feature '+ str(i+1) for i in range(len(Oil_Prod_prepared[0]))] # Make a list for columns (Features)
Oil_Prod_pd = pd.DataFrame(Oil_Prod_prepared, columns=Feature_list)
Oil_Prod_p_target=pd.concat([Oil_Prod_pd, Oil_Prod_Target], axis=1)
Oil_Prod_p_target[0:5]
Then we split the training set to as 85% smaller training set and 15% validation set.
# Split the training set to 15% varidation set and smaller traning set
Smaller_training, Validation = train_test_split(Oil_Prod_p_target, test_size=0.15, random_state=40)
You should remove target columns ("OIL Prod. (e3m3/month)") from the smaller training and validation set and have them as separate data.
# Assign target values for retitived data.
Smaller_Target=Smaller_training["OIL Prod. (e3m3/month)"]
Validation_Target=Validation["OIL Prod. (e3m3/month)"]
# Remove "OIL Prod. (e3m3/month)" that is the target from list
Smaller_training = Smaller_training.drop("OIL Prod. (e3m3/month)", axis=1)
Validation = Validation.drop("OIL Prod. (e3m3/month)", axis=1)
Both small training and validation set are fed to Machine Learning. First train Decision Tree model with the small training and then test it with validation set.
# Apply Decision Tree for smaller training set
dtree_reg.fit(Smaller_training, Smaller_Target)
Oil_Prod_predictions = dtree_reg.predict(Smaller_training)
tree_mse = mean_squared_error(Smaller_Target, Oil_Prod_predictions)
tree_rmse = np.round(np.sqrt(tree_mse),5)
tree_rmse
Again Decision Tree has perfectly predict all values of smaller training set. Now the trained Decision Tree model is applied to predict validation set to see if this is overfitting or not. Notice the Decision Tree model has not seen validation set before.
# Apply trained Decision Tree for validation set
Oil_Prod_predictions = dtree_reg.predict(Validation)
tree_mse = mean_squared_error(Validation_Target, Oil_Prod_predictions)
tree_rmse = np.round(np.sqrt(tree_mse),5)
tree_rmse
Yes. It is proved that the Decision Tree model is overfitting since it gives very bad performance on the unseen data set (Validation), worse than linear regression.
Reliable Evaluation with K-Fold Cross-Validation¶
K-fold cross-validation is a reliable technique to evaluate your model; it applies a number of folds to provide each segment of data a chance to serve as both the validation and training set. First data are divided into number of folds, for example 6 folds in Figure below; then a model is trained with 5 folds and 1 folds is used for validation: every time a different fold is considered for evaluation. The result is 6 predictions using different data for trainings and validations.
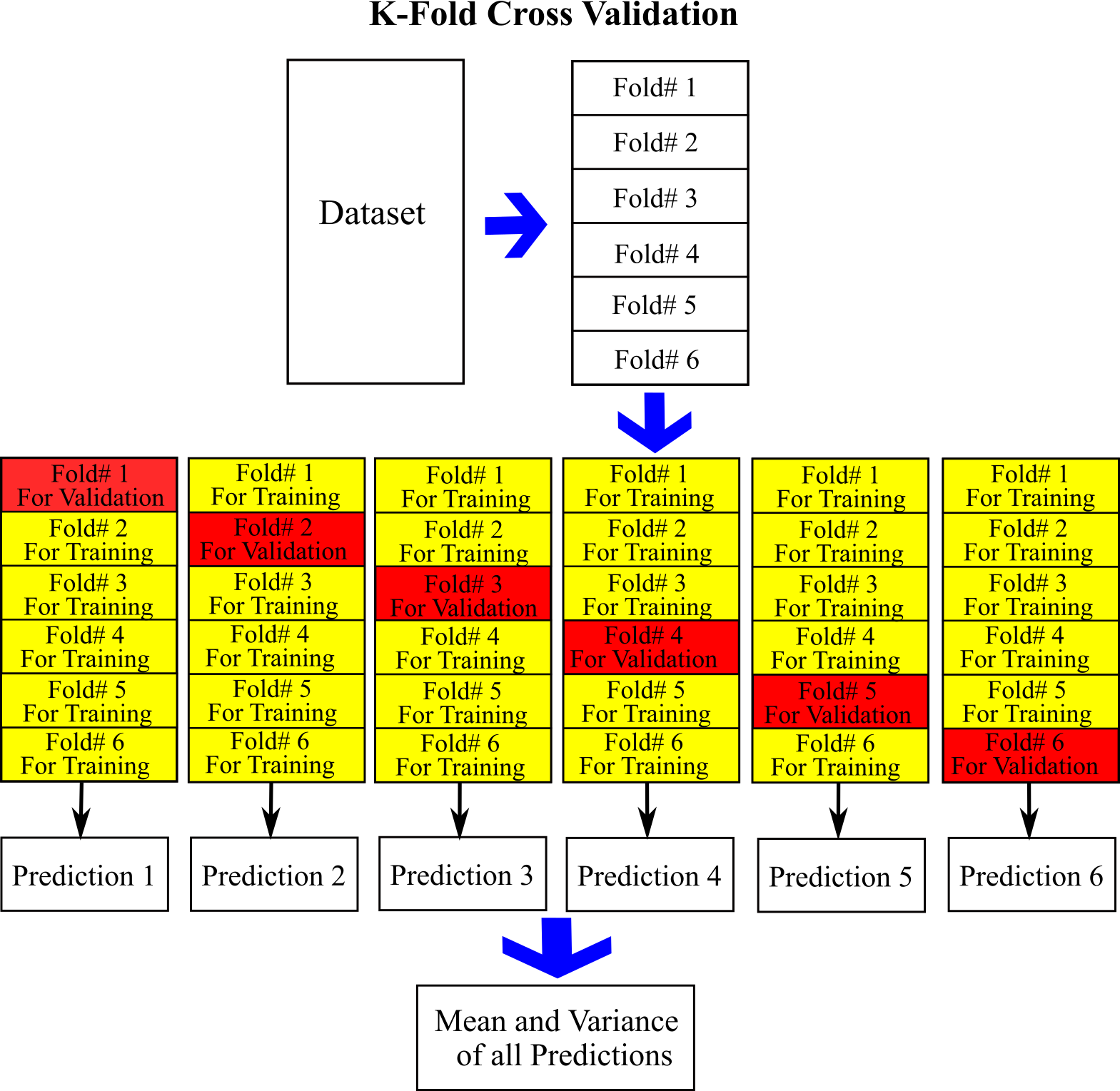
The mean $m_{R}$ and variance $\sigma_{R}^{2}$ of the Root Mean Square Error ($RMSE$) for each set can be calculated to quantify uncertainty in predictive model.
$\sigma_{R} ^{2}=\frac{1}{n}\sum_{i=1}^{n}\left (R_{i}-m_{R} \right )^2$
then you can use a confidence interval to tell how confident your prediction (see Figure below).
- 68.0% of the predictions fall within 1 standard deviation of $\large m_{R} \pm \sigma_{R}$
- 95.0% of the predictions fall within 2 standard deviation of $\large m_{R} \pm 2\sigma_{R}$
- 99.7% of the predictions fall within 3 standard deviation of $\large m_{R} \pm 3\sigma_{R}$
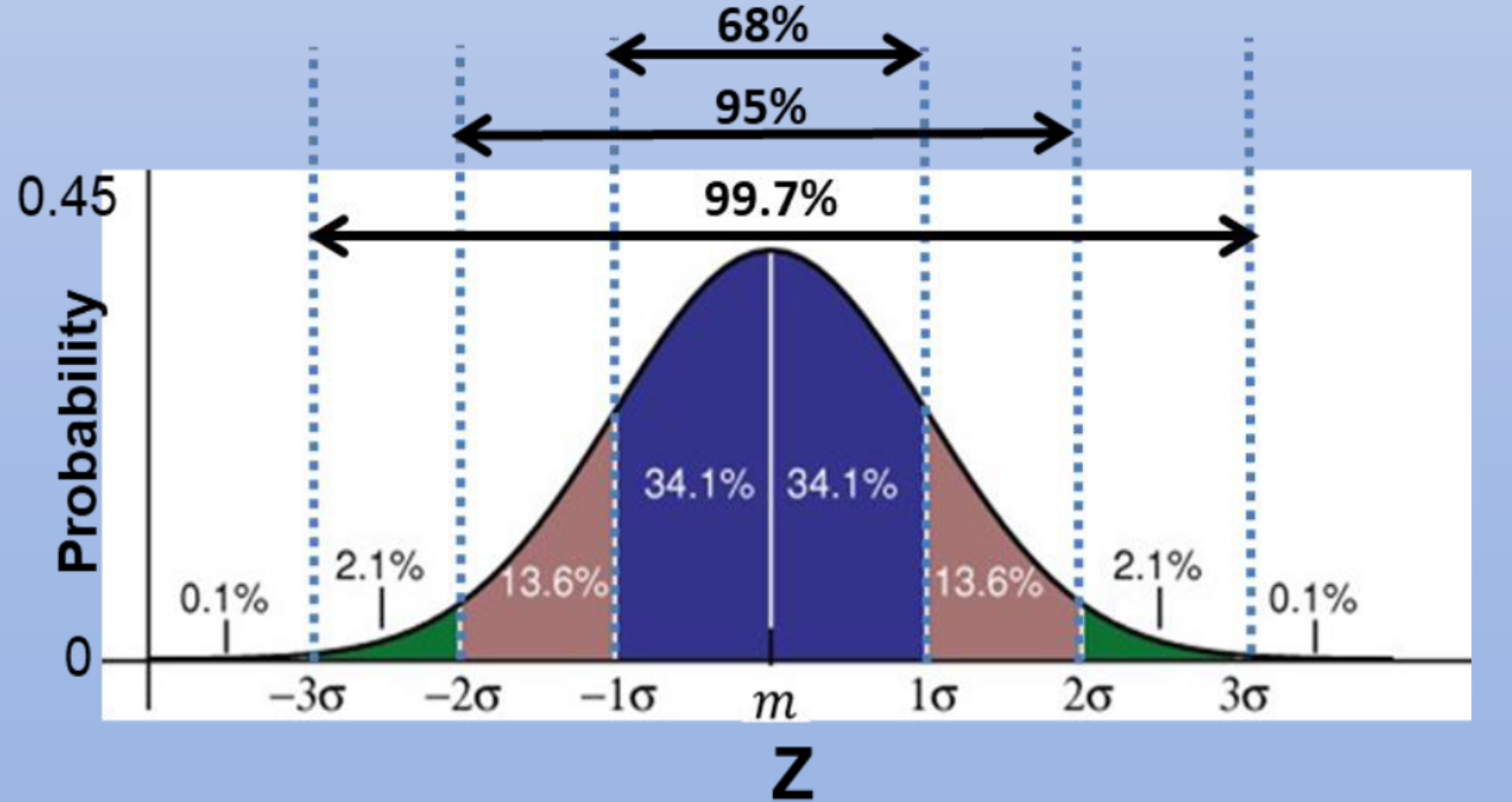
see here for more information.
You need larger fold (say bigger than 20) to have a reliable uncertainty assessment. This approach is much better than simply divide the training set into smaller training set and validation set. The only problem is using cross-validation with high fold for large data set can be computationally expensive.
Scikit-Learn has K-fold cross-validation function. The following code randomly splits the training set into 20 folds, then it trains and evaluates the Decision Tree model 20 times, by selecting a different fold for evaluation every time and training on the other 19 folds.
Scikit-Learn’s cross-validation feature assumes greater is better rather than a cost function: lower is better. The scoring function gives negative values for mean square error. So we need to multiply scores by -1 before calculating the square root. The following code shows cross validation for 50 folds for Linear Regression and Decision Tree models.
from sklearn.model_selection import cross_val_score
scores = cross_val_score(lin_reg, Oil_Prod_prepared, Oil_Prod_Target,scoring="neg_mean_squared_error", cv=50)
linreg_rmse_scores = np.sqrt(-scores)
scores = cross_val_score(dtree_reg, Oil_Prod_prepared, Oil_Prod_Target,scoring="neg_mean_squared_error", cv=50)
dtree_rmse_scores = np.sqrt(-scores)
The Figure below shows histogram of RMSE for Linear Regression and Decision Tree models
font = {'size' : 9}
matplotlib.rc('font', **font)
fig = plt.subplots(figsize=(10, 3), dpi= 150, facecolor='w', edgecolor='k')
ax1=plt.subplot(1,2,1)
val=linreg_rmse_scores
histplt(val,bins=16,title='Histogram of RMSE_Linear Regression',xlabl=' RMSE ',xlimt=(24,58),axt=ax1)
ax2=plt.subplot(1,2,2)
val=dtree_rmse_scores
histplt(val,bins=14,title='Histogram of RMSE_Decision Tree Model',xlabl=' RMSE ',xlimt=(24,58),axt=ax2)
The cross-validation allows you to get not only an estimate of the performance of your model, but also a measure of how precise this estimate is (i.e., its standard deviation). The histograms shows that 68.0% of RMSE for Linear Regression model falls within 35.2$\pm$ 4.2 and but for Decision Tree 68.0% of RMSE falls within 43.0$\pm$ 4.0; so Decision Tree performs worse than the Linear Regression model! If you just used one validation set, you would not have this information. However, cross-validation comes at the cost of training the model several times that may not possible for all data set. Cross validation will be very computationally expensive for large data set.
Try Complex Models to Improve Performance¶
We should try several models to see which one gives better prediction. We have not discussed the models yet but let's try the Random Forest. We will discuss it in details in the coming lectures; here we just want to apply a more complex model to see how the results change. Random Forests work by training many Decision Trees using a random subsets of the features, then aggregating the predictions (averaging). See the code below to apply K-fold cross validation using Random Forest.
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor()
scores = cross_val_score(forest_reg, Oil_Prod_prepared, Oil_Prod_Target,scoring="neg_mean_squared_error", cv=50)
forest_reg_scores = np.sqrt(-scores)
#forest_reg_scores
font = {'size' : 9}
matplotlib.rc('font', **font)
fig = plt.subplots(figsize=(9, 3), dpi= 120,facecolor='w', edgecolor='k')
ax1=plt.subplot(1,2,1)
val=forest_reg_scores
histplt(val,bins=9,title='Histogram of RMSE_Random Forest',xlabl=' RMSE ',xlimt=(24,58),axt=ax1)
Yes, Random Forest looks promising although we only used default hyperparameters. The histograms of cross-validation shows that 68.0% of RMSE for Random Forestn model falls within 30.8$\pm$ 2.5 which has both lower mean and standard deviation compared with Linear Regression and Decision Tree; we will explain how to fine-tune your model using Scikit-Learn to get higher performance. So, if we apply other complex models, we can get higher performance.
Try to Remove Irrelevant Features or Add New Features¶
Another way to improve the performance of your model is to remove irrelevant features or add new features. For example, we might want to remove the columns "Surface-Casing Weight (kg/m)" "Production-Casing Size (mm)", "Production-Casing Weight (kg/m)" since they may not have that much impact on oil production. See the code below:
Oil_Prod_prepared_new=np.delete(Oil_Prod_prepared, [4,5,6], axis=1)
scores = cross_val_score(lin_reg, Oil_Prod_prepared_new, Oil_Prod_Target,scoring="neg_mean_squared_error", cv=50)
linreg_rmse_scores = np.sqrt(-scores)
scores = cross_val_score(dtree_reg, Oil_Prod_prepared_new, Oil_Prod_Target,scoring="neg_mean_squared_error", cv=50)
dtree_rmse_scores = np.sqrt(-scores)
font = {'size' : 9}
matplotlib.rc('font', **font)
fig = plt.subplots(figsize=(10, 3), dpi= 150, facecolor='w', edgecolor='k')
ax1=plt.subplot(1,2,1)
val=linreg_rmse_scores
histplt(val,bins=16,title='Histogram of RMSE_Linear Regression',xlabl=' RMSE ',xlimt=(24,58),axt=ax1)
ax2=plt.subplot(1,2,2)
val=dtree_rmse_scores
histplt(val,bins=14,title='Histogram of RMSE_Decision Tree Model',xlabl=' RMSE ',xlimt=(24,58),axt=ax2)
Removing those features did not improve performance of Linear Regression and Decision Tree. We can try removing other features to see if any improvement achieved or not. Moreover, other features can be added to the dataset to improve performance.
Evaluate Final Model on the Test Set¶
By working on training set and tweaking the models, you should achieve a final model that you are satisfied with its performance. The last step is to evaluate the final model on the test set that your model has never before seen this dataset. You do not need to do anything special about this process, only get the features and labels from your test data set; you should apply the same data preparation and transformation for test set. Notice you only need to call transform() not fit_transform. It means, for example, missing values in test set should be imputed using the information from training set. This process should be applied for other transformation such as standardization.
# Remove target
Oil_Prod_test = test_set_strat.drop("OIL Prod. (e3m3/month)", axis=1)
Oil_Prod_Target_test = test_set_strat["OIL Prod. (e3m3/month)"].copy()
# Imputation
Oil_Prod_num = Oil_Prod_test.drop(["Deviation (True/False)","Prod. Formation"], axis=1)
im = imput_mdn.transform(Oil_Prod_num)
Oil_Prod_im = pd.DataFrame(im, columns=Oil_Prod_num.columns)
# Deal with text
# Categorical Feature 1: "Prod. Formation"
Oil_Prod_cat = Oil_Prod_test[["Prod. Formation"]]
cat_encoder = OneHotEncoder()
Oil_Prod_cat_1hot = cat_encoder.fit_transform(Oil_Prod_cat)
cat_hot_toarray_1=Oil_Prod_cat_1hot.toarray()
# Categorical Feature 2 (Deviation (True/False))
Oil_Prod_cat = Oil_Prod_test[["Deviation (True/False)"]]
Oil_Prod_cat_2hot = cat_encoder.fit_transform(Oil_Prod_cat)
cat_hot_toarray_2=Oil_Prod_cat_2hot.toarray()
# Standardization
Oil_Prod_im_MMS=Oil_Prod_im.copy()
Oil_Prod_im_Std=scaler.fit_transform(Oil_Prod_im_MMS)
Oil_Prod_im_Std
# Concatenate Scaled and One-hot Encoded Feature
Oil_Prod_prepared_test=np.concatenate((Oil_Prod_im_Std,cat_hot_toarray_1, cat_hot_toarray_2), axis=1)
Lets apply linear regression for test data set and calculate RMSE:
Oil_Prod_predictions = lin_reg.predict(Oil_Prod_prepared_test)
mse_lin = mean_squared_error(Oil_Prod_Target_test, Oil_Prod_predictions)
rmse_lin= np.sqrt(mse_lin)
rmse_lin
Most of the time, this estimation may be sufficient as the generalization error. You might want to have an idea of how precise this estimate is. For example, you may want to know what is the range of generalized error for a 95% confidence interval:in other words, what is uncertainty in the mean of your error. But how we can calculate the distribution of the mean error since we have only one mean of error computed from data. It can be calculated based on Central Limit Theorem that says for a large enough sample size n, the distribution of the sampling mean will approach a normal distribution.. Ok that is good. We now know the the distribution of the sampling mean is Gaussian (normal) based on Central Limit Theorem. The mean of the sampling distribution is the mean of the population. Therefore, if a population has a mean $\mu$, then the mean of the sampling distribution is also $\mu_{s}$: $\mu=\mu_{s}$. The variance of the sampled mean is calculated by:
$\large\sigma^{2}_{\mu_{s}}=\frac{\sigma^{2}}{n_{ind}}$ where $\sigma^{2}$ is the variance of data and $n_{ind}$ is number of independent data.
For example, 95% of the mean falls within:
$\large \mu\pm 2 \sqrt{\frac{\sigma^{2}}{n_{ind}}}$
So we can calculate the uncertainty in the mean of error for 95% confidence interval using the equation above:
squared_errors = (Oil_Prod_Target_test-Oil_Prod_predictions)**2
m=np.mean(squared_errors) # mean of squared error
vr= np.var(squared_errors) # Variance of squared error
sd_m=np.sqrt(vr/(len(Oil_Prod_predictions)))
print('Upper limit of the mean: ',np.round(np.sqrt(m+2*sd_m),1)) # 95% confidence interval
print('Lower limit of the mean: ',np.round(np.sqrt(m-2*sd_m),1)) # 95% confidence interval
You can also apply scipy package to simply calculate the range of error for any given confidence interval.
from scipy import stats
confidence = 0.95
squared_errors = (Oil_Prod_Target_test- Oil_Prod_predictions) ** 2
interval=stats.t.interval(confidence, len(squared_errors),loc=squared_errors.mean(),
scale=stats.sem(squared_errors))
print('Upper limit of the mean: ',np.round(np.sqrt(interval)[1],1)) # 95% confidence interval
print('Lower limit of the mean: ',np.round(np.sqrt(interval)[0],1)) # 95% confidence interval
You may achieve lower performance on test set than what you calculate by cross-validation since you probably apply a lot of hyperparameter tuning: this leads your system ends up fine-tuned to perform well on the validation data, and will likely not perform as well on never-before seen dataset. For this example, it was not the case since we have not tuned hyperparameters. But, even if you see this in your project, you must resist the temptation to change and tweak the hyperparameters in order to get higher performance on the test set since the improvements may not be applied for new data. Each time you tweak the parameter, the so called information leak will happen and you will end-up an model that seems very promising but performs very bad on new data set.