Summary
A more efficient imputation technique is developed by LU (lower–upper) simulation in this work: (lower–upper) triangular decomposition of the correlation matrix. Cholesky factorization is applied on correlation (covariance) matrix between features and missing data are imputed via conditioning on non-missing values. The relationships between features are reproduced and the associated uncertainty in missing data are quantified after imputation. This approach requires less computational power for large datasets. In this post, Python code is implemented to apply the technique on synthetic data and realistic data.
Python functions and data files needed to run this notebook are available via this link.
import pandas as pd
import numpy as np
import matplotlib
import pylab as plt
from matplotlib.ticker import PercentFormatter
from functions import* # import require functions to run this notebook
import math
Table of Contents
- 1 Methodology
- 2 Generate Synthetic Data with Missing Values
- 3 Cross plot Matrix
- 4 Correlation Matrix and Percentage of Missing for Bivariate
- 5 Percentage of Missing Values
- 6 Imputation with LU Conditional Simulation
- 7 Simple Imputation with Median
- 8 Feature 1 vs. Feature 2
- 9 Feature 2 vs. Feature 3
- 10 Realistic Example
Methodology¶
Missing data occur when no data value is stored for the variable in an observation. Missing data is one of the main challenges faced by machine learning. There are some approaches in practice to deal with missing values: 1- Drop column: one naive approach is to remove columns that have missing values. This approach is not reliable since the information of other columns without missing data is removed from dataset. 2- Drop row: another approach is to remove rows that have missing data. This approach is also not recommend because number of data (rows) is decreased that leads to loss of information. 3- Replace with Median or Mean: a common practice is to replace missing values with the median (mean) value for that column. However, this may also lead to unreliable prediction and artifacts since a large population of data would have similar values. The K nearest neighbours (K-NN) is an algorithm that applies feature similarity. Missing data are imputed by finding the K’s closest neighbours. K-NN is sensitive to outliers. It also does not consider the uncertainty in missing values. Bootstrapping can be applied to quantify uncertainty in distribution of each feature, and then replace each missing value with a random sample from the distribution. Although this approach measures the uncertainty, the correlation between features cannot be reproduced after imputation. The correlations and statistics (mean and standard deviation) should be honored after imputation. There are other techniques that respect the correlation after imputations such as multivariate imputation by chained equation (MICE) and deep learning. However, imputation can be quite slow and computationally expensive for large datasets. An imputation technique that can quantify associated uncertainty in missing data is developed in this Section. We propose imputing missing data using LU simulation: (lower–upper) triangular decomposition of the correlation matrix. Many theoretical developments of LU simulation have taken place in geo-statistics for geomodeling and spatial resampling. A modified LU conditional simulation (Davis 1987) is proposed for imputation in this paper by conditioning non-missing values to impute missing data for each well. This approach respects the correlation between features and quantifies uncertainty in missing values. It is also very fast requiring much less computational power for large data sets. The procedure is summarized by:
Normal Score Transformation. Quantile-quantile transformation is applied to convert distribution of each feature to Gaussian distribution.
Correlation Matrix of Features. Figure below shows a schematic illustration of correlation matrix $\boldsymbol{\rho}$ for $n$ features. The diagonal elements of this correlation matrix $\boldsymbol{\rho_{11}},\boldsymbol{\rho_{22}},....,\boldsymbol{\rho_{nn}}$ are 1: the correlation of each feature to itself.
Cholesky Decomposition. The correlation matrix can be discomposed by Cholesky decomposition as $\boldsymbol{\rho}=\textbf{LU}$. Figure below shows lower triangular matrix $\textbf{L}$ achieved from Cholesky decomposition.
Modified LU Conditional Simulation. A vector of uncorrelated standard normal deviate $\mathbf{w}$ with mean=0, standard deviation=1 is simulated for each feature. The length of $\mathbf{w}$ for each feature is number of data (here is total number of wells for training set). LU unconditional simulation can be simply calculated by $\textbf{y}=\textbf{Lw}$. Figure below-b shows how to generate LU unconditional simulation achieving correlated Gaussian realization $\textbf{y}$. For conditioning non-missing features, each array of $\mathbf{w}$ vector with known values should be converted to $\mathbf{w^{c}}$ that is a function of the non-missing features. The main challenge for this modified LU simulation is the ordering of missing and non--missing features for each row of data. If non--missing values are placed first followed by missing data, the conditioning will be applied. So, non--missing values are required to be placed first followed by missing data for each instance (row of data). This requires reconstructing the correlation matrix for each instance to be consistent with the order of features. This ordering is not important within missing and non--missing features.
Back-transform from Gaussian to Original Space. The simulated values in Gaussian space should be back-transformed to original space.
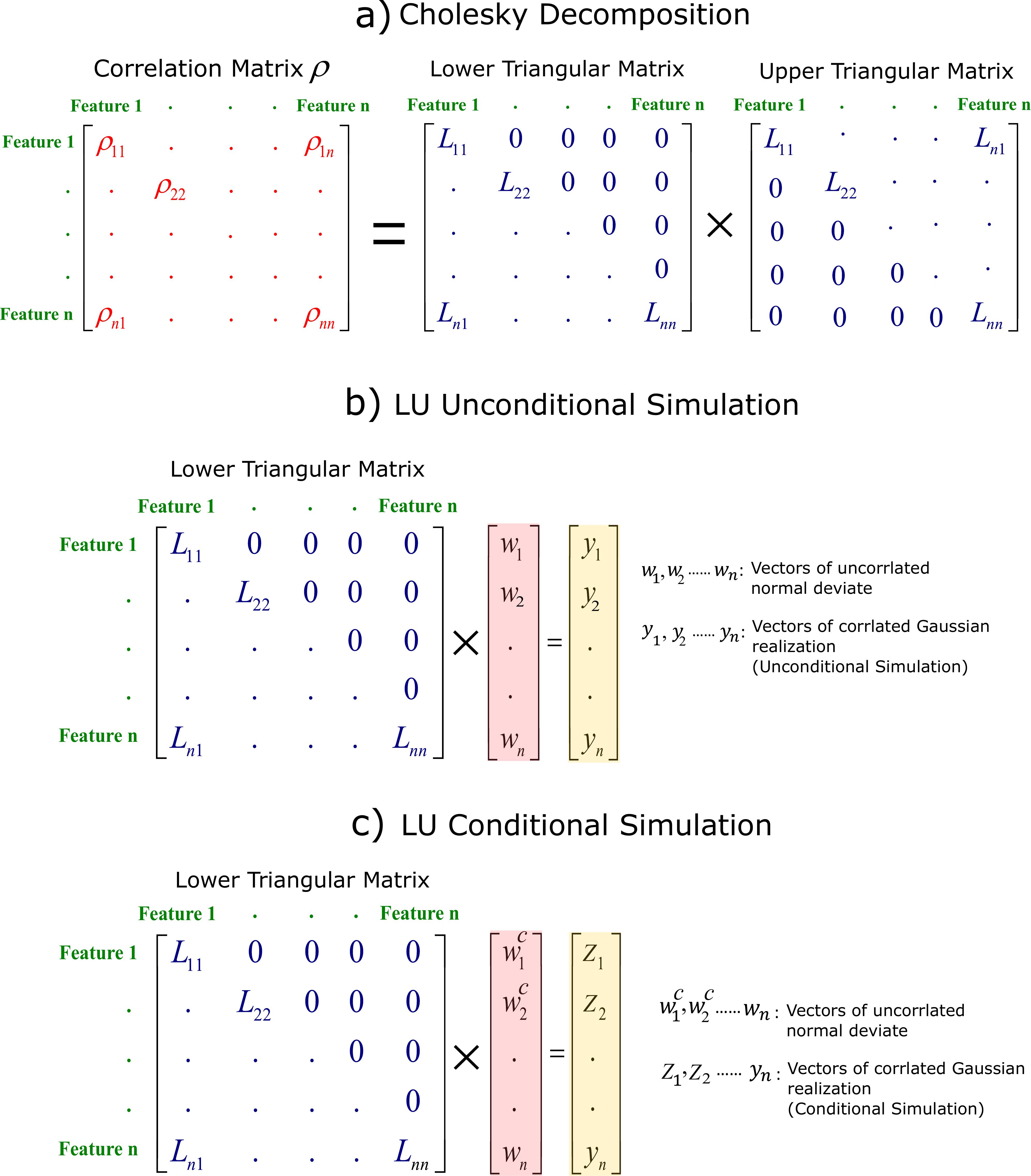
Last two steps are repeated for all data in training set to impute all missing data. Due to random sampling from distribution of each feature, this approach quantifies uncertainty in missing data while respecting the correlation between features. Moreover, implementation of the steps above is straightforward (especially with Python programming language). See the implementation below:
Generate Synthetic Data with Missing Values¶
Code below generates synthetic data with missing values. There are 4 features that are correlated with each other.
# Make a synthetic correlation matric for 4 propeties
corr=np.zeros((4,4))
corr[0,0]=corr[1,1]=corr[2,2]=corr[3,3]=1.0
corr[0,1]=corr[1,0]=0.25
corr[0,2]=corr[2,0]=0.471
corr[0,3]=corr[3,0]=-0.43
#
corr[0,1]=corr[1,0]=0.62
corr[0,2]=corr[2,0]=0.34
corr[0,3]=corr[3,0]=0.42
#
corr[1,2]=corr[2,1]=-0.44
corr[1,3]=corr[3,1]=0.64
#
corr[2,3]=corr[3,2]=-0.54
# Make synthetic data for simulation
nsim=10000 # number of simulation
val=[]
mu=5; sigma=1
# Normal distribution
val.append(np.random.normal(mu, sigma, nsim))
# Lognormal distribution
val.append(np.random.lognormal(0.58, 0.5, nsim))
# Triangular distribution
val.append(np.random.triangular(0,2.5, 5, nsim))
# Triangular distribution
val.append(np.random.triangular(0,0.5, 5, nsim))
# Order the random distributions of variable to respect the correlation between them
np.random.seed(42)
matrix=corr
L=scipy.linalg.cholesky(matrix, lower=True, overwrite_a=True)
mu=0; sigma=1; nvar=len(matrix)
w=np.zeros((nvar,nsim))
for i in range (nvar):
for j in range(nsim):
Dist = np.random.normal(mu, sigma, nsim)
w[i,:]=Dist
Sim_R_val=[]
N_var=[]
for i in range(nsim):
tmp=(np.matmul(L,w[:,i]))
N_var.append(tmp)
N_var=np.array(N_var).transpose()
#
Sim_R_val=[]
for i1 in range(nvar):
R_tmp=np.zeros(len(val[i1]))
tmp=np.sort(N_var[i1])
tmp_1=np.sort(val[i1])
for i2 in range(nsim):
index1=np.where(N_var[i1]==tmp[i2])[0]
index2=np.where(val[i1]==tmp_1[i2])[0]
R_tmp[index1[0]]=val[i1][index2[0]]
Sim_R_val.append(R_tmp)
#
columns=['Feature ' +str(i+1) for i in range(4)]
df=pd.DataFrame({columns[0]:np.array(Sim_R_val[0]),columns[1]:np.array(Sim_R_val[1]),
columns[2]:np.array(Sim_R_val[2]),columns[3]:np.array(Sim_R_val[3])},columns=columns)
np.random.seed(42)
df['Feature 1'].iloc[np.random.permutation(df.index)[:2800]]=np.nan
np.random.seed(52)
df['Feature 2'].iloc[np.random.permutation(df.index)[:3200]]=np.nan
np.random.seed(62)
df['Feature 3'].iloc[np.random.permutation(df.index)[:2200]]=np.nan
np.random.seed(72)
df['Feature 4'].iloc[np.random.permutation(df.index)[:1400]]=np.nan
Cross plot Matrix¶
Figure below shows cross plot matrix and histogram of features on diagonal arrays. Percentage of missing values are shown on each histogram.
font = {'size' :12 }
plt.rc('font', **font)
fig=plt.figure(figsize=(10, 9), dpi= 80, facecolor='w', edgecolor='k')
# Make cross plot matrix
cplotmatrix(df,alpha=0.05,marker='ro',font=font)
Correlation Matrix and Percentage of Missing for Bivariate¶
Figure below shows correlation matrix on lower matrix and percentage of missing values on upper matrix:
# Plot covariance matrix between 5 variables with positive and negative linear correlations
font = {'size' : 7.5}
matplotlib.rc('font', **font)
fig, ax=plt.subplots(figsize=(3, 3), dpi= 200, facecolor='w', edgecolor='k')
#
corr=df.corr().to_numpy()
colmn=list(df.columns)
for i in range(len(df.columns)):
for j in range(len(df.columns)):
if i>=j:
c=corr[j,i]
ax.text(j, i, str(round(c,2)), va='center', ha='center',fontsize=10)
cax =ax.matshow(corr, cmap='jet', interpolation='nearest',vmin=-0.8, vmax=0.8)
cbaxe_ = fig.add_axes([0.20, 0.01, 0.6, 0.030])
fig.colorbar(cax,cax=cbaxe_,shrink=0.7,label='Correlation Coefficient',orientation='horizontal')
ax.set_xticks(np.arange(len(colmn)))
ax.set_xticklabels(colmn,fontsize=8.5, rotation=25)
ax.set_yticks(np.arange(len(colmn)))
ax.set_yticklabels(colmn,fontsize=8.5, rotation=65)
# Missing matrix between features excluding x and y
Per_NaN=np.zeros((len(colmn),len(colmn)))
for j in range(len(colmn)):
for i in range(len(colmn)):
New_pd=pd.concat([df[[colmn[i]]],df[[colmn[j]]]],axis=1)
New_pd_=(New_pd.dropna(subset=[colmn[i],colmn[j]])).to_numpy()
Per_NaN[i,j]=100-(len(New_pd_)/len(New_pd))*100
Per_NaN[j,i]=np.nan
for j in range(len(colmn)):
for i in range(len(colmn)):
if j<=i:
c=Per_NaN[j,i]
if(i!=j): ax.text(i, j, str(int(c))+'%', va='center', ha='center',fontsize=10,c='w')
im =ax.matshow(Per_NaN, cmap='Greys', interpolation='nearest',vmin=0, vmax=100)
cbaxe_ = fig.add_axes([0.95, 0.2, 0.03, 0.60])
fig.colorbar(im,cax=cbaxe_,label='Percentage of Missing Data \n for each Bivariate',orientation='vertical')
#plt.text(-2800,150,' Matrix of Correlation and Missing Data', fontsize=10)
plt.show()
Percentage of Missing Values¶
#Calculate number of missing data and percentage for each feature
per_non_nan=[]
non_nan_=[]
Colms=df.columns
for i in range(len(Colms)):
non_nan=df[Colms[i]].count()
non_nan_.append(len(df)-non_nan)
per_non_nan.append(float(100-(non_nan/len(df))*100))
#Sort percentage of missing data and columns
sort_array=np.sort(per_non_nan)
sort_colms=[]
uniqu=list(np.unique(per_non_nan))
for i in range(len(uniqu)):
ind=[j for j, x in enumerate(per_non_nan) if x == uniqu[i]]
for k in ind:
sort_colms.append(Colms[k])
#Sort number of missing data and columns
sort_non_nan_=np.sort(non_nan_)
sort_non_nan__=[]
uniqu=list(np.unique(non_nan_))
for i in range(len(uniqu)):
ind=[j for j, x in enumerate(non_nan_) if x == uniqu[i]]
for k in ind:
sort_non_nan__.append(Colms[k])
#Plot barchart with two vertical axis
font = {'size' : 10}
matplotlib.rc('font', **font)
fig, ax1 = plt.subplots(figsize=(8, 4), dpi= 200, facecolor='w', edgecolor='k')
width=0.4
ax2 = ax1.twinx() # Create another axes that shares the same x-axis
index1 = np.arange(len(sort_colms))
index2 = np.arange(len(sort_non_nan__))
ax1.bar(index1, sort_array,color='b',width=width,linewidth=0.9,edgecolor='k')
ax2.bar(index2, sort_non_nan_,color='b',width=width,linewidth=0.9,edgecolor='k')
plt.title('Percentage and Number of Missing Values for each Variable',fontsize=12)
ax1.set_ylabel('Percentage of Missing Data (%)',fontsize='9.5')
ax2.set_ylabel('Number of Missing Data',fontsize='9.5')
ax1.set_xticks(np.arange(len(Colms)))
ax1.set_xticklabels(sort_colms,fontsize=12, rotation=0)
ax1.xaxis.grid(color='r', linestyle='--', linewidth=1) # horizontal lines
plt.show()
Imputation with LU Conditional Simulation¶
cond_LU_Sim automatically applies conditional LU to simulate missing values conditioning non-missing values.
%%time
df_im=cond_LU_Sim(df,seed=34)
font = {'size' :14 }
plt.rc('font', **font)
fig=plt.figure(figsize=(10, 8), dpi= 80, facecolor='w', edgecolor='k')
cplotmatrix(df_im,alpha=0.05,marker='go',missin_rep=False, font=font)
plt.show()
Simple Imputation with Median¶
Imputation with simple median of each feature is calculated to compare with conditional LU simulation.
clmn=list(df.columns)
df_im_m=pd.DataFrame()
for iclm in clmn:
P50=df[iclm].median() # Calculate median of each column
df_im_m[iclm]=df[iclm].fillna(P50) # replace NaN with median(P50)
font = {'size' :14 }
plt.rc('font', **font)
fig=plt.figure(figsize=(10, 9), dpi= 80, facecolor='w', edgecolor='k')
# Make cross plot matrix
ind=df.loc[(df.isnull()['Feature 1']) | (df.isnull()['Feature 2']) |
(df.isnull()['Feature 3']) | (df.isnull()['Feature 4'])].index
df_im_new=df_im_m.iloc[ind]
cplotmatrix(df_im_new,alpha=0.05,marker='go',missin_rep=False, font=font)
plt.show()
Simple imputation with median have to constants values on cross plots and the correlation between features after imputation are not preserved. This can lead to problem when this data is used for prediction.
Feature 1 vs. Feature 2¶
Now we can look closely between features before and after imputation with median and conditional LU simulation.
font = {'size' :11}
#
plt.rc('font', **font)
fig=plt.figure(figsize=(9, 8), dpi= 100, facecolor='w', edgecolor='k')
col_1=0
col_2=1
colm_=list(df.columns)
markersize=5
gs = gridspec.GridSpec(2, 4)
ax1=plt.subplot(gs[0, :2], )
ind_na=df.loc[~(df.isnull()[colm_[col_1]]) & ~(df.isnull()[colm_[col_2]])].index
x=np.array(df[columns[col_1]].iloc[ind_na])
y=np.array(df[columns[col_2]].iloc[ind_na])
n_x=len(x)
Mean_x=np.mean(x)
SD_x=np.sqrt(np.var(x))
#
n_y=len(y)
Mean_y=np.mean(y)
SD_y=np.sqrt(np.var(y))
corr=np.corrcoef(x,y)
txt=r'$\rho_{x,y}}$=%.2f'+'\n $n$=%.0f \n $\mu_{x}$=%.0f \n $\sigma_{x}$=%.0f \n '
txt+=' $\mu_{y}$=%.0f \n $\sigma_{y}$=%.0f'
anchored_text = AnchoredText(txt %(corr[1,0], n_x,Mean_x,SD_x,Mean_y,SD_y), loc=2,
prop={ 'size': font['size']*1.1, 'fontweight': 'bold'})
plt.plot(x,y,'ro',markersize=markersize,alpha=0.5,label='Not Missing')
ax1.add_artist(anchored_text)
plt.legend(framealpha =1, loc=1,markerscale=1.5)
plt.xlabel(columns[col_1],fontsize=font['size']*1.2)
plt.ylabel(columns[col_2],fontsize=font['size']*1.2)
plt.title('Before Imputation',fontsize=font['size']*1.3)
ax1=plt.subplot(gs[0, 2:])
plt.plot(x,y,'ro',markersize=markersize,alpha=0.2,label='Not Missing')
x_1=np.array(df_im[columns[col_1]])
y_1=np.array(df_im[columns[col_2]])
n_x=len(x_1)
Mean_x=np.mean(x_1)
SD_x=np.sqrt(np.var(x_1))
#
n_y=len(y_1)
Mean_y=np.mean(y_1)
SD_y=np.sqrt(np.var(y_1))
corr=np.corrcoef(x_1,y_1)
txt=r'$\rho_{x,y}}$=%.2f'+'\n $n$=%.0f \n $\mu_{x}$=%.0f \n $\sigma_{x}$=%.0f \n '
txt+=' $\mu_{y}$=%.0f \n $\sigma_{y}$=%.0f'
anchored_text = AnchoredText(txt %(corr[1,0], n_x,Mean_x,SD_x,Mean_y,SD_y), loc=2,
prop={ 'size': font['size']*1.1, 'fontweight': 'bold'})
ind_na=df.loc[(df.isnull()[columns[col_1]]) | (df.isnull()[columns[col_2]])].index
x_2=np.array(df_im[columns[col_1]].iloc[ind_na])
y_2=np.array(df_im[columns[col_2]].iloc[ind_na])
plt.plot(x_2,y_2,'g*',markersize=markersize*1.6,label='Imputed',alpha=0.2)
ax1.add_artist(anchored_text)
plt.legend(framealpha =1, loc=1,markerscale=1.5)
plt.xlabel(columns[col_1],fontsize=font['size']*1.2)
plt.ylabel(columns[col_2],fontsize=font['size']*1.2)
plt.title('Imputation by LU Conditional Simulation',fontsize=font['size']*1.3)
ax1=plt.subplot(gs[1, 1:3])
df_=df.copy()
ind=df.loc[(df.isnull()['Feature '+str(i)]) | (df.isnull()['Feature '+str(j)])].index
x1=df_[colm_[i]].iloc[ind]
y1=df_[colm_[j]].iloc[ind]
plt.plot(x,y,'ro',markersize=markersize,alpha=0.2,label='Not Missing')
mdin=df_[colm_[col_1]].median()
df_[colm_[col_1]]=df_[colm_[col_1]].fillna(mdin)
mdin=df_[colm_[j]].median()
df_[colm_[col_2]]=df_[colm_[col_2]].fillna(mdin)
x_1=np.array(df_[columns[col_1]])
y_1=np.array(df_[columns[col_2]])
n_x=len(x_1)
Mean_x=np.mean(x_1)
SD_x=np.sqrt(np.var(x_1))
#
n_y=len(y_1)
Mean_y=np.mean(y_1)
SD_y=np.sqrt(np.var(y_1))
corr=np.corrcoef(x_1,y_1)
txt=r'$\rho_{x,y}}$=%.2f'+'\n $n$=%.0f \n $\mu_{x}$=%.0f \n $\sigma_{x}$=%.0f \n '
txt+=' $\mu_{y}$=%.0f \n $\sigma_{y}$=%.0f'
anchored_text = AnchoredText(txt %(corr[1,0], n_x,Mean_x,SD_x,Mean_y,SD_y), loc=2,
prop={ 'size': font['size']*1.1, 'fontweight': 'bold'})
ind_na=df.loc[(df.isnull()[columns[col_1]]) | (df.isnull()[columns[col_2]])].index
x_2=np.array(df_[columns[col_1]].iloc[ind_na])
y_2=np.array(df_[columns[col_2]].iloc[ind_na])
plt.plot(x_2,y_2,'g*',markersize=markersize*1.6,label='Imputed',alpha=0.2)
ax1.add_artist(anchored_text)
plt.legend(framealpha =1, loc=1,markerscale=1.5)
plt.xlabel(columns[col_1],fontsize=font['size']*1.2)
plt.ylabel(columns[col_2],fontsize=font['size']*1.2)
plt.title('Imputation by Median',fontsize=font['size']*1.3)
fig.tight_layout(pad=1.5)
plt.subplots_adjust(wspace=0.5)
plt.show()
Feature 2 vs. Feature 3¶
font = {'size' :11}
#
plt.rc('font', **font)
fig=plt.figure(figsize=(9, 8), dpi= 100, facecolor='w', edgecolor='k')
col_1=1
col_2=2
colm_=list(df.columns)
markersize=5
gs = gridspec.GridSpec(2, 4)
ax1=plt.subplot(gs[0, :2], )
ind_na=df.loc[~(df.isnull()[colm_[col_1]]) & ~(df.isnull()[colm_[col_2]])].index
x=np.array(df[columns[col_1]].iloc[ind_na])
y=np.array(df[columns[col_2]].iloc[ind_na])
n_x=len(x)
Mean_x=np.mean(x)
SD_x=np.sqrt(np.var(x))
#
n_y=len(y)
Mean_y=np.mean(y)
SD_y=np.sqrt(np.var(y))
corr=np.corrcoef(x,y)
txt=r'$\rho_{x,y}}$=%.2f'+'\n $n$=%.0f \n $\mu_{x}$=%.0f \n $\sigma_{x}$=%.0f \n '
txt+=' $\mu_{y}$=%.0f \n $\sigma_{y}$=%.0f'
anchored_text = AnchoredText(txt %(corr[1,0], n_x,Mean_x,SD_x,Mean_y,SD_y), loc=4,
prop={ 'size': font['size']*1.1, 'fontweight': 'bold'})
plt.plot(x,y,'ro',markersize=markersize,alpha=0.5,label='Not Missing')
ax1.add_artist(anchored_text)
plt.legend(framealpha =1, loc=1,markerscale=1.5)
plt.xlabel(columns[col_1],fontsize=font['size']*1.2)
plt.ylabel(columns[col_2],fontsize=font['size']*1.2)
plt.title('Before Imputation',fontsize=font['size']*1.3)
ax1=plt.subplot(gs[0, 2:])
plt.plot(x,y,'ro',markersize=markersize,alpha=0.2,label='Not Missing')
x_1=np.array(df_im[columns[col_1]])
y_1=np.array(df_im[columns[col_2]])
n_x=len(x_1)
Mean_x=np.mean(x_1)
SD_x=np.sqrt(np.var(x_1))
#
n_y=len(y_1)
Mean_y=np.mean(y_1)
SD_y=np.sqrt(np.var(y_1))
corr=np.corrcoef(x_1,y_1)
txt=r'$\rho_{x,y}}$=%.2f'+'\n $n$=%.0f \n $\mu_{x}$=%.0f \n $\sigma_{x}$=%.0f \n '
txt+=' $\mu_{y}$=%.0f \n $\sigma_{y}$=%.0f'
anchored_text = AnchoredText(txt %(corr[1,0], n_x,Mean_x,SD_x,Mean_y,SD_y), loc=4,
prop={ 'size': font['size']*1.1, 'fontweight': 'bold'})
ind_na=df.loc[(df.isnull()[columns[col_1]]) | (df.isnull()[columns[col_2]])].index
x_2=np.array(df_im[columns[col_1]].iloc[ind_na])
y_2=np.array(df_im[columns[col_2]].iloc[ind_na])
plt.plot(x_2,y_2,'g*',markersize=markersize*1.6,label='Imputed',alpha=0.2)
ax1.add_artist(anchored_text)
plt.legend(framealpha =1, loc=1,markerscale=1.5)
plt.xlabel(columns[col_1],fontsize=font['size']*1.2)
plt.ylabel(columns[col_2],fontsize=font['size']*1.2)
plt.title('Imputation by LU Conditional Simulation',fontsize=font['size']*1.3)
ax1=plt.subplot(gs[1, 1:3])
df_=df.copy()
ind=df.loc[(df.isnull()['Feature '+str(i)]) | (df.isnull()['Feature '+str(j)])].index
x1=df_[colm_[i]].iloc[ind]
y1=df_[colm_[j]].iloc[ind]
plt.plot(x,y,'ro',markersize=markersize,alpha=0.2,label='Not Missing')
mdin=df_[colm_[col_1]].median()
df_[colm_[col_1]]=df_[colm_[col_1]].fillna(mdin)
mdin=df_[colm_[j]].median()
df_[colm_[col_2]]=df_[colm_[col_2]].fillna(mdin)
x_1=np.array(df_[columns[col_1]])
y_1=np.array(df_[columns[col_2]])
n_x=len(x_1)
Mean_x=np.mean(x_1)
SD_x=np.sqrt(np.var(x_1))
#
n_y=len(y_1)
Mean_y=np.mean(y_1)
SD_y=np.sqrt(np.var(y_1))
corr=np.corrcoef(x_1,y_1)
txt=r'$\rho_{x,y}}$=%.2f'+'\n $n$=%.0f \n $\mu_{x}$=%.0f \n $\sigma_{x}$=%.0f \n '
txt+=' $\mu_{y}$=%.0f \n $\sigma_{y}$=%.0f'
anchored_text = AnchoredText(txt %(corr[1,0], n_x,Mean_x,SD_x,Mean_y,SD_y), loc=4,
prop={ 'size': font['size']*1.1, 'fontweight': 'bold'})
ind_na=df.loc[(df.isnull()[columns[col_1]]) | (df.isnull()[columns[col_2]])].index
x_2=np.array(df_[columns[col_1]].iloc[ind_na])
y_2=np.array(df_[columns[col_2]].iloc[ind_na])
plt.plot(x_2,y_2,'g*',markersize=markersize*1.6,label='Imputed',alpha=0.2)
ax1.add_artist(anchored_text)
plt.legend(framealpha =1, loc=1,markerscale=1.5)
plt.xlabel(columns[col_1],fontsize=font['size']*1.2)
plt.ylabel(columns[col_2],fontsize=font['size']*1.2)
plt.title('Imputation by Median',fontsize=font['size']*1.3)
fig.tight_layout(pad=1.5)
plt.subplots_adjust(wspace=0.5)
plt.show()
Realistic Example¶
Consider the data file "Auto_MPG_Data.csv" retrieved from UCI Machine Learning repository. This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University. The dataset was used in the 1983 American Statistical Association Exposition. The missing values are imputed by the developed technique.
df = pd.read_csv("./Data/Auto_MPG_Data.csv") # Read data file
df
Correlation Matrix¶
# Plot covariance matrix between 5 variables with positive and negative linear correlations
font = {'size' : 6}
matplotlib.rc('font', **font)
fig, ax=plt.subplots(figsize=(3, 3), dpi= 200, facecolor='w', edgecolor='k')
#
corr=df.corr().to_numpy()
colmn=list(df.columns)
for i in range(len(df.columns)):
for j in range(len(df.columns)):
if i>=j:
c=corr[j,i]
ax.text(j, i, str(round(c,2)), va='center', ha='center',fontsize=7)
cax =ax.matshow(corr, cmap='jet', interpolation='nearest',vmin=-0.9, vmax=0.9)
cbaxe_ = fig.add_axes([0.20, 0.01, 0.6, 0.030])
fig.colorbar(cax,cax=cbaxe_,shrink=0.7,label='Correlation Coefficient',orientation='horizontal')
ax.set_xticks(np.arange(len(colmn)))
ax.set_xticklabels(colmn,fontsize=6.5, rotation=90)
ax.set_yticks(np.arange(len(colmn)))
ax.set_yticklabels(colmn,fontsize=6.5, rotation=0)
# Missing matrix between features excluding x and y
Per_NaN=np.zeros((len(colmn),len(colmn)))
for j in range(len(colmn)):
for i in range(len(colmn)):
New_pd=pd.concat([df[[colmn[i]]],df[[colmn[j]]]],axis=1)
New_pd_=(New_pd.dropna(subset=[colmn[i],colmn[j]])).to_numpy()
Per_NaN[i,j]=100-(len(New_pd_)/len(New_pd))*100
Per_NaN[j,i]=np.nan
for j in range(len(colmn)):
for i in range(len(colmn)):
if j<=i:
c=Per_NaN[j,i]
if(i!=j): ax.text(i, j, str(int(c))+'%', va='center', ha='center',fontsize=7,c='w')
im =ax.matshow(Per_NaN, cmap='Greys', interpolation='nearest',vmin=0, vmax=100)
cbaxe_ = fig.add_axes([0.95, 0.2, 0.03, 0.60])
fig.colorbar(im,cax=cbaxe_,label='Percentage of Missing Data \n for each Bivariate',orientation='vertical')
plt.text(-25,160,' Matrix of Correlation and Missing Data', fontsize=8)
plt.show()
Cross plot Matrix¶
font = {'size' :8.5 }
plt.rc('font', **font)
fig=plt.figure(figsize=(12, 9), dpi= 80, facecolor='w', edgecolor='k')
# Make cross plot matrix
cplotmatrix(df,alpha=0.1,marker='ro',loc=3,scale=1.2,font=font,missin_rep=False)
Imputation with LU Conditional Simulation¶
%%time
df_im=cond_LU_Sim(df,seed=34, col_in=['Cylinders'])
Correlation Matrix¶
# Plot covariance matrix between 5 variables with positive and negative linear correlations
font = {'size' : 6}
matplotlib.rc('font', **font)
fig, ax=plt.subplots(figsize=(3, 3), dpi= 200, facecolor='w', edgecolor='k')
#
corr=df_im.corr().to_numpy()
colmn=list(df_im.columns)
for i in range(len(df_im.columns)):
for j in range(len(df_im.columns)):
if i>=j:
c=corr[j,i]
ax.text(j, i, str(round(c,2)), va='center', ha='center',fontsize=7)
cax =ax.matshow(corr, cmap='jet', interpolation='nearest',vmin=-0.9, vmax=0.9)
cbaxe_ = fig.add_axes([0.20, 0.01, 0.6, 0.030])
fig.colorbar(cax,cax=cbaxe_,shrink=0.7,label='Correlation Coefficient',orientation='horizontal')
ax.set_xticks(np.arange(len(colmn)))
ax.set_xticklabels(colmn,fontsize=6.5, rotation=90)
ax.set_yticks(np.arange(len(colmn)))
ax.set_yticklabels(colmn,fontsize=6.5, rotation=0)
# Missing matrix between features excluding x and y
Per_NaN=np.zeros((len(colmn),len(colmn)))
for j in range(len(colmn)):
for i in range(len(colmn)):
New_pd=pd.concat([df_im[[colmn[i]]],df_im[[colmn[j]]]],axis=1)
New_pd_=(New_pd.dropna(subset=[colmn[i],colmn[j]])).to_numpy()
Per_NaN[i,j]=100-(len(New_pd_)/len(New_pd))*100
Per_NaN[j,i]=np.nan
for j in range(len(colmn)):
for i in range(len(colmn)):
if j<=i:
c=Per_NaN[j,i]
if(i!=j): ax.text(i, j, str(int(c))+'%', va='center', ha='center',fontsize=7,c='w')
im =ax.matshow(Per_NaN, cmap='Greys', interpolation='nearest',vmin=0, vmax=100)
cbaxe_ = fig.add_axes([0.95, 0.2, 0.03, 0.60])
fig.colorbar(im,cax=cbaxe_,label='Percentage of Missing Data \n for each Bivariate',orientation='vertical')
plt.text(-28,160,' Matrix of Correlation and Missing Datan after Imputation', fontsize=7)
plt.show()
Cross plot Matrix¶
font = {'size' :8 }
plt.rc('font', **font)
fig=plt.figure(figsize=(10, 9), dpi= 120, facecolor='w', edgecolor='k')
cplotmatrix(df_im,alpha=0.1,marker='go',loc=3,scale=1.3, font=font)
plt.show()