Summary
Customer churn is a financial expression referring to losing of a customer or client when a customer abandons interaction with business or company. Churn rate is defined as the rate of customers leaving a company within a specific time duration. Low churn rate can be an indicator of success for companies so they try to retain as many customers as they can. With the advent of machine learning deep learning techniques, companies can identify potential customers who may stop doing business with them in the near future. Strategies can be applied to retain those costumers. In this notebook, customer churn is predicted for a bank based on different customer attributes including geography, age, gender, income and more. a wide range of predictive algorithms and various performance metrics were considered to achieve the most reliable classifier.
Python functions and data files needed to run this notebook are available via this link.
import os
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from functions import* # import require functions to run this notebook
from IPython.display import HTML
import pickle
import logging
import matplotlib.patheffects as pe
import matplotlib.ticker as mtick
import warnings
warnings.filterwarnings('ignore')
Table of Contents
- 1 Methodology
- 2 Data Processing
- 3 Predictive Models
- 4 ROC Chart for Training set
- 5 Performance of the Models on Training Set
- 6 Test Set
- 7 Train Final Model with all Data
Methodology¶
A binary classification will be applied Churn_Modelling.csv downloaded from Kaggle: the target feature is Exited (0 and 1). The following steps will be applied:
- The irrelevant features are removed from data (we do not need customer's name, customer's ID). The linear correlation between features and target are calculated or run Random Forest analysis to rank the importance of features to predict the target.
- The data set is divided into 80% training set and 20% test set. The test set is only applied at the end as a never-before-seen dataset to only evaluate the trained models and make sure the models are not overfitted and no information leaks occur (see Figure below).
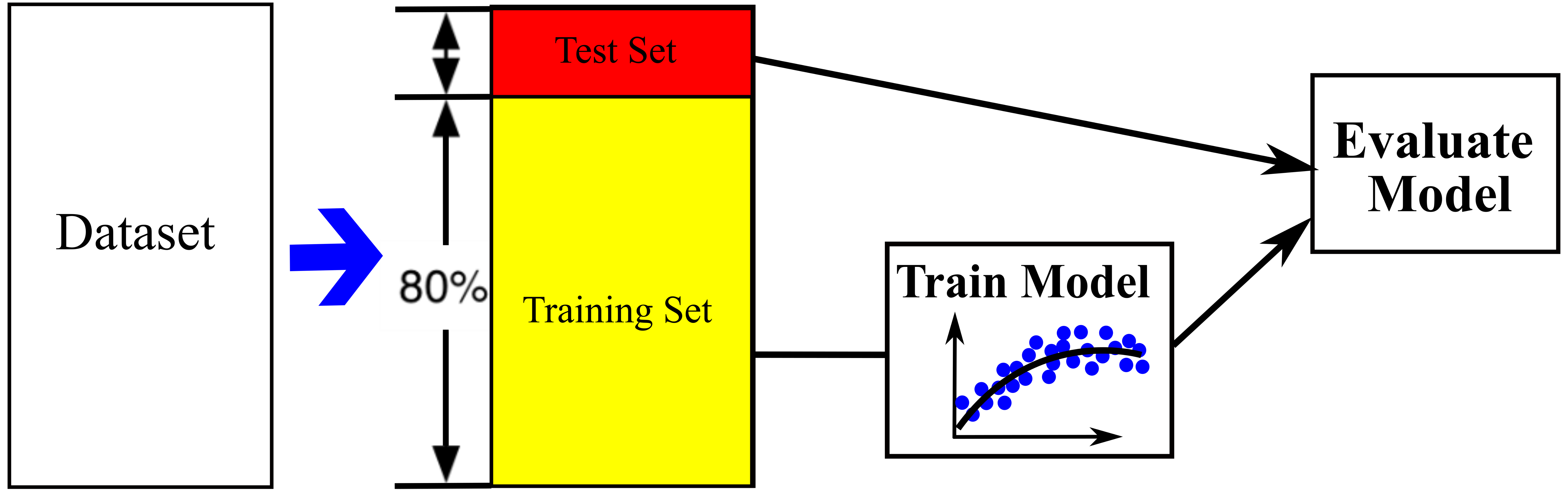
- Data processing is applied for training set including imputation of missing values, normalization and text handling. The data is clean up and get ready to feed ML algorithms.
- Train ML algorithms mentioned above using the training set by implementing a binary classification. Each algorithm is optimized by fine-tuning the hyperparameters. To avoid overfitting, K-fold cross validation is applied. The training set (we do not touch test set) into 3-folds (k=3); each model is trained with 2 folds and apply prediction for 1-folds. The process is repeated for all 3 folds to apply prediction for all training set. This leads to prevent overfitting and have a clean prediction (See Figure below). Therefore, performance of the algorithms can be measured for the training set and compared with other since the same data is fed to each algorithms.
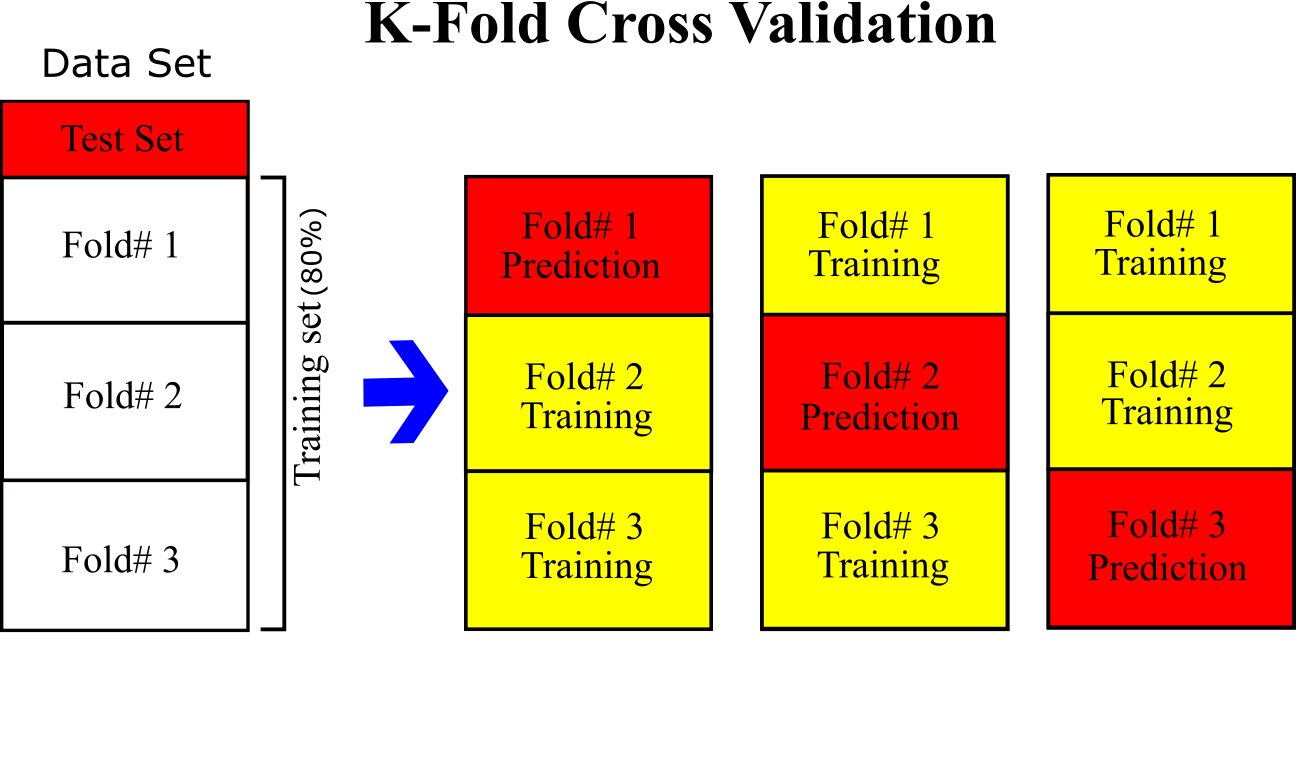
- The trained models are applied to predict test set to confirm the performances make sure there is no overfitting. The models have not seen the test sets during the training so the resulted performance for test set can be an indication of performance for future prediction of these models. The same data processing for training set should be applied for test set. The same statistics for imputation of training set should be applied for test set.
Data Processing¶
The data set Churn_Modelling.csv can be downloaded from Kaggle named.
# Read data 'Churn_Modelling.csv'
df = pd.read_csv('./Data/Churn_Modelling.csv')
# Shuffle the data
np.random.seed(32)
df=df.reindex(np.random.permutation(df.index))
df.reset_index(inplace=True, drop=True) # Reset index
# Remove 'RowNumber','CustomerId','Surname' features
df=df.drop(['RowNumber','CustomerId','Surname'],axis=1,inplace=False)
Divide Data into Training set (80%) and Test set (20%)¶
font = {'size' : 9.5}
plt.rc('font', **font)
fig = plt.subplots(figsize=(10, 3), dpi= 150, facecolor='w', edgecolor='k')
ax1=plt.subplot(1,2,1)
bins = np.array([-0.05,0.05,0.95,1.05])
EDA_plot.histplt (df['Exited'],bins=bins,title='Percentage of Churn (0) or Retain (1) Customers',xlabl="",
ylabl='Percentage',xlimt=(-0.1,1.1),ylimt=(0,0.9),axt=ax1,x_tick=[0,1],
scale=1.1,loc=1,font=8,color='#8DC63F')
plt.show()
# Training and Test
spt = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_idx, test_idx in spt.split(df, df['Exited']):
train_set_strat = df.loc[train_idx]
test_set_strat = df.loc[test_idx]
train_set_strat.reset_index(inplace=True, drop=True) # Reset index
test_set_strat.reset_index(inplace=True, drop=True) # Reset index
font = {'size' : 10}
plt.rc('font', **font)
fig = plt.subplots(figsize=(10, 3), dpi= 160, facecolor='w', edgecolor='k')
ax1=plt.subplot(1,2,1)
val=train_set_strat['Exited']
EDA_plot.histplt(val,bins=bins,title="Training Set (80% of Data)",xlabl="",
ylabl='Percentage',xlimt=(-0.1,1.1),ylimt=(0,0.9),axt=ax1,x_tick=[0,1],
scale=1.2,loc=1,font=8,color='y')
ax2=plt.subplot(1,2,2)
val=test_set_strat['Exited']
EDA_plot.histplt(val,bins=bins,title="Test Set (20% of Data)",xlabl="",
ylabl='Percentage',xlimt=(-0.1,1.1),ylimt=(0,0.9),axt=ax2,x_tick=[0,1],
scale=1.2,loc=1,font=8,color='b')
plt.subplots_adjust(wspace=0.25)
plt.show()
Text Handeling¶
'Geography' and 'Gender' features are text that are converted to numbers via one-hot-encoding.
# Convert Geography to one-hot-encoding
Geog_1hot=pd.get_dummies(train_set_strat['Geography'],prefix='Geography')
# Convert gender to 0 and 1
ordinal_encoder = OrdinalEncoder()
train_set_strat['Gender'] = ordinal_encoder.fit_transform(train_set_strat[['Gender']])
# Remove 'Geography'
train_set_strat=train_set_strat.drop(['Geography'],axis=1,inplace=False)
train_set_strat=pd.concat([Geog_1hot,train_set_strat], axis=1) # Concatenate rows
train_set_strat
Impute Missing Values¶
Check if there is missing values.
train_set_strat.info()
There is no missing value.
# Correlation matrix
font = {'size' : 11}
plt.rc('font', **font)
fig, ax=plt.subplots(figsize=(8, 8), dpi= 110, facecolor='w', edgecolor='k')
df_tmp=train_set_strat.drop(['Geography_France','Geography_Germany','Geography_Spain'], axis=1)
corr_array=Correlation_plot.corr_mat(df_tmp,corr_val_font=8,
title=f'Correlation Matrix between {len(df_tmp.columns)} Features'
,titlefontsize=12,xy_title=[1,-3.5],xyfontsize = 10,vlim=[-1, 1],axt=ax)
Figure below show correlation between training features and target feature (Exited). Age has positive correlation and IsActiveMember has negative correlation with target (Exited). Other Features are not linearly correlated with the target (Exited).
font = {'size' : 5.5}
plt.rc('font', **font)
ax1 = plt.subplots(figsize=(3.2, 3.5), dpi= 200, facecolor='w', edgecolor='k')
# Plot correlations of attributes with the last column
target='Exited'
corr=df_tmp.corr()
corr=corr[target].drop([target])
coefs=corr.values
clmns=list(corr.index)
Correlation_plot.corr_bar(coefs,clmns=clmns,yfontsize=6.0,xlim=[-0.4,0.4],
title=f'Linear Correlation with {target}',ymax_vert_lin=30)
Standardization¶
# Make training features and target
X_train = train_set_strat.drop("Exited", axis=1)
y_train = train_set_strat["Exited"].values
# Divide into two training sets (with and without standization)
clmn=['Geography_France','Geography_Germany','Geography_Spain',
'Gender','NumOfProducts','HasCrCard','IsActiveMember']
X_train_for_std = X_train.drop(clmn, axis=1)
X_train_not_std =X_train[clmn]
features_colums=list(X_train_for_std.columns)+list(X_train_not_std.columns)
# Standadization
scaler = StandardScaler()
scaler.fit(X_train_for_std)
# Standardization for training set
df_train_std=scaler.transform(X_train_for_std)
fname = './Trained_Models/scaler.sav'
pickle.dump(scaler, open(fname, 'wb'))
X_train_std=np.concatenate((df_train_std,X_train_not_std), axis=1)
X_train_std
# Divide training data into smaller training and validation
# Training set
Training_c=np.concatenate((X_train_std,y_train.reshape(-1,1)),axis=1)
Smaller_Training, Validation = train_test_split(Training_c, test_size=0.2, random_state=100)
Smaller_Training_Target=Smaller_Training[:,-1]
Smaller_Training=Smaller_Training[:,:-1]
# Validation set
Validation_Target=Validation[:,-1]
Validation=Validation[:,:-1]
# Number of predictors and make empty arrays
predictor= ['Dummy Classifier','Stocastic Gradient Descent','Logistic Regression',
'Support Vector Machine','Decision Trees','Adaptive Gradient Boosting',
'Random Forest','Neural Network']
filename=["" for x in range(len(predictor))]
# Creat Empty List for Avergae Accuracy for each regressor
Predict_training=np.zeros(len(predictor))
pre_prob=[]
Train_Accu=np.zeros(len(predictor)); Train_Rec=np.zeros(len(predictor));Train_Pre=np.zeros(len(predictor));Train_Spe=np.zeros(len(predictor))
Test_Accu=np.zeros(len(predictor)); Test_Rec=np.zeros(len(predictor));Test_Pre=np.zeros(len(predictor));Test_Spe=np.zeros(len(predictor))
Predictive Models¶
A wide range of machine learning algorithms from basic to advanced methods. A brief explanation of each is as follows:
- Stochastic Gradient Descent (SGD) is a good place to start. Gradient descent is a general idea to minimize a cost function by iteratively tweaking parameters. It has a wide range of application to find optimal solutions for many problems. It computes the gradient of the cost function regarding model parameters and updates the parameters through iteration until a global minimum of cost function is reached. Gradient Descent (and mini-batch) can be very slow for large data set: Stochastic Gradient Descent is efficient because it just picks a random instance at every iteration and computes the gradients based only on that single instance.
- Logistic Regression (LR) is a simple approach to estimate the probability of a particular class. It calculates a weighted sum of the input features (plus a bias term) and use sigmoid function to estimate probability of each class. It has been commonly used for medical science and health and failure detection in engineering.
- Support Vector Machine (SVM) is a powerful algorithm to perform linear or nonlinear classification.It is highly preferred since less computation power is required to produce reliable accuracy.The fundamental idea is to have the largest possible margin between the classes. It predicts theclass of a new instance by computing a decision function with optimum parameters.
- Decision Trees (DT) is a reliable ML algorithms and has been widely applied to solve complex and non-linear problems for both classification and regression. It is the fundamental component of Random Forest: it is applied based on a flowchart structure in which each node denotes a test, each branch represents the result of the test, and each leaf node represents a class label.
- Random Forest (RF) is among the most versatile and reliable machine learning algorithms for non-linear and complex data. The RF randomly creates and merges multiple decision trees and predicts a class that gets the most votes among all trees. Despite its simplicity, RF is one of the most powerful ML algorithms available today.
- Adaptive Boosting (AB) can be applied for any predictor mentioned above to enhance the performance and turn into a stronger learner. The general idea is to use a base classifier and apply on training set first, then corrects base classifier by paying attention to the training instances that are underfitted. This leads to a new classifier focusing more on the hard cases. The process of training a classifier repeated sequentially, each classifier trying to correct its predecessor.
- Neural Network is a specific subfield of machine learning for tackling a very complex problem. In comparison with Shallow Neural Network, Deep Neural Network usually involves much more successive layers of representations that are learned from training data. The large network’s architecture may lead to some problems such as vanishing/exploding gradients, overfitting, computational cost and slow training. However, these problems can be resolved by tuning some hyperparameters. Deep Neural Network has been recently applied in many disciplines including computer vision, speech recognition, natural language processing, audio recognition and so on.
- Ensemble Learning usually applies near the end of project when a few good and promising predictors are built to integrate them into an even stronger predictor. It works by aggregating the predictions of a group of predictors. RF and AB can be categorized as EL. A very simple EL is hard voting (HV) that aggregates the predictions of each classifier and predicts the class that gets the most votes. Soft voting (SV) is another EL that works by averaging the probability of each class and predict a class with the highest probability. It often achieves higher performance than HV due to giving more weight to highly confident votes. Instead of using simple functions to aggregate the predictions of all predictors, staking approach (SA) trains a model to perform this aggregation. The final predictor takes these predictions as inputs and makes the final prediction. EL may lead to even better prediction than the best individual if predictors are independent from each other (Géron 2019).
The performance of all seven algorithms are measured for both training set and test set compared with a Dummy Classifier for sanity check. This classifier is useful as a simple baseline to compare with other (real) classifiers. The ML algorithms for this work are retrieved from Scikit-Learn and Tensorflow Libraries.
Performance Measurement¶
The most common approach for assessment of classification is accuracy, which is calculated by number of true predicted over total number of data. However, accuracy alone may not be practical for performance measurement of classifiers, especially in cease of skewed datasets. Accuracy should be considered along with other metrics. Confusion matrix is a much better way to evaluate the performance of a classifier. The general idea is to consider the number of times instances of negative class are misclassified as positive class and vice versa. Three more metrics Sensitivity, Precision and Specificity can be calculated as well as Accuracy:
Accuracy=(𝑇𝑃+𝑇𝑁)/(𝑇𝑃+𝑇𝑁+𝐹𝑃+𝐹𝑁): Accuracy is simply the fraction of the total samples that is correctly identified.
Sensitivity (Recall)= 𝑇𝑃/(𝑇𝑃+𝐹𝑁): Sensitivity is the proportion of correct positive predictions to the total positive classes.
Precision= 𝑇𝑃/(𝑇𝑃+𝐹𝑃): Precision is the proportion of correct positive prediction to the total predicted values.
Specificity= 𝑇𝑁/(𝑇𝑁+𝐹𝑃) Specificity is the true negative rate or the proportion of negatives that are correctly identified.
TP: True Positives, FP: False Positives, FN: False Negatives, TN: True Negatives
Another common approach to measure performance is the receiver operating characteristic (ROC). The ROC curve plots the true positive rate (Sensitivity) against the false positive rate (1-Specificity). Every point on the ROC curve represents a chosen cut-off even though it cannot be seen. For more information and details see ROC. The most common way to compare classifiers is to measure the area under the curve (AUC). A perfect classifier will have a ROC AUC equal to 1, whereas a purely random classifier will have a ROC AUC equal to 0.5 (See Figure below).
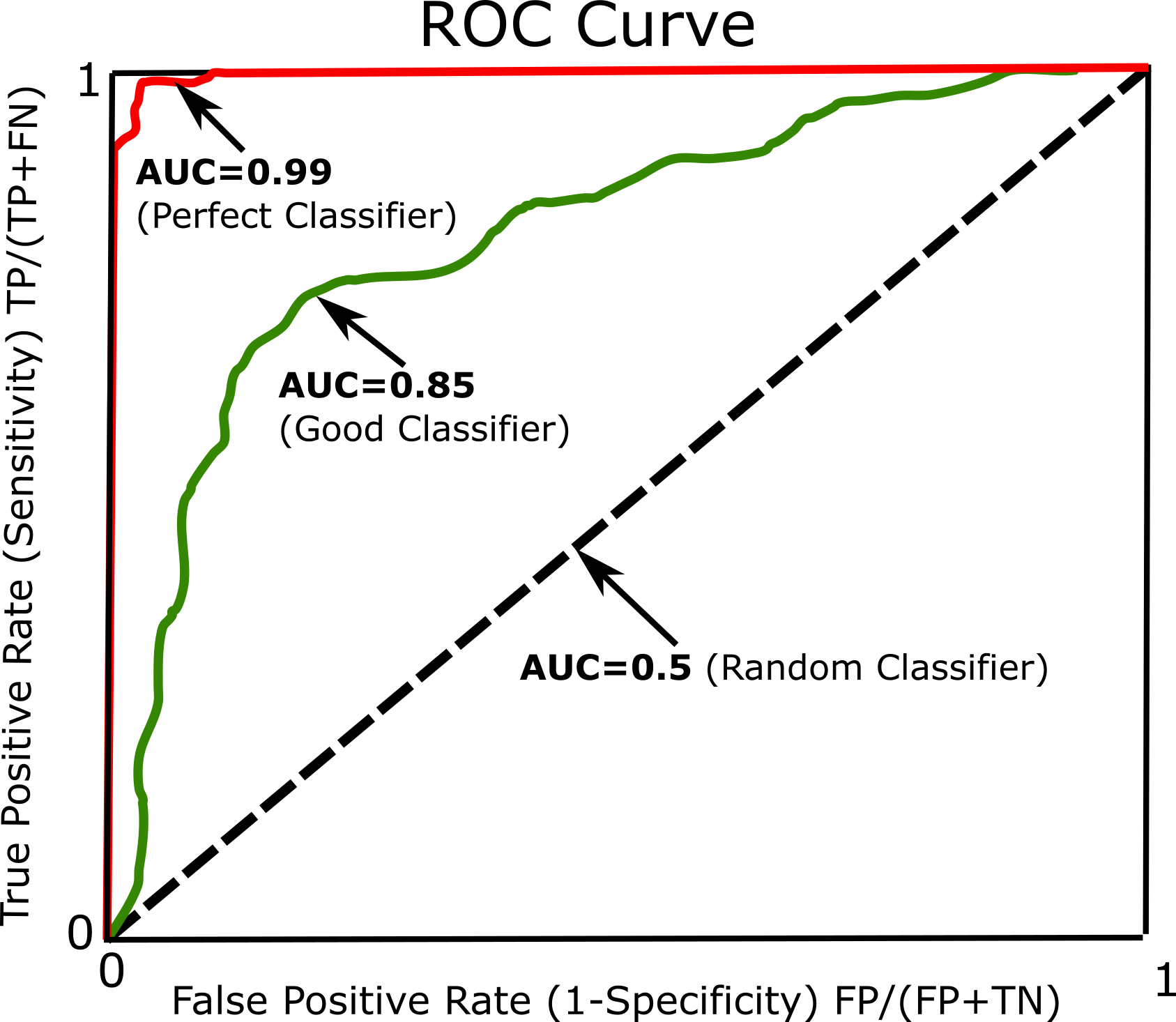
Dummy Classifier¶
dmy_clf = DummyClassifier(random_state=42)
dmy_clf.fit(X_train_std,y_train)
y_train_pred=cross_val_predict(dmy_clf,X_train_std,y_train, cv=3)
y_train_proba_dc=cross_val_predict(dmy_clf,X_train_std,y_train, cv=3, method='predict_proba')
font = {'size' : 6}
plt.rc('font', **font)
fig = plt.subplots(figsize=(5, 5), dpi= 250, facecolor='w', edgecolor='k')
ax1=plt.subplot(1,2,1)
i=0
tmp1,tmp2,tmp3,tmp4=prfrmnce_plot.Conf_Matrix(y_train,y_train_pred.reshape(-1,1),axt=ax1,
t_fontsize=6,x_fontsize=5,y_fontsize=5,title='Dummy Classifier')
Train_Accu[i]=tmp1; Train_Pre[i]=tmp2; Train_Rec[i]=tmp3; Train_Spe[i]=tmp4
# save the model to disk
filename[i] = './Trained_Models/dmy_clf.sav'
pickle.dump(dmy_clf, open(filename[i], 'wb'))
Stochastic Gradient Descent¶
sgd_clf = SGDClassifier(random_state=42,loss='log')
sgd_clf.fit(X_train_std,y_train)
y_train_pred=cross_val_predict(sgd_clf,X_train_std,y_train, cv=3)
y_train_proba_sgd=cross_val_predict(sgd_clf,X_train_std,y_train, cv=3, method='predict_proba')
font = {'size' : 6}
plt.rc('font', **font)
fig = plt.subplots(figsize=(5, 5), dpi= 250, facecolor='w', edgecolor='k')
ax1=plt.subplot(1,2,1)
i=1
tmp1,tmp2,tmp3,tmp4=prfrmnce_plot.Conf_Matrix(y_train,y_train_pred.reshape(-1,1),axt=ax1,t_fontsize=6,x_fontsize=5,
y_fontsize=5,title='Stochastic Gradient Descent')
Train_Accu[i]=tmp1; Train_Pre[i]=tmp2; Train_Rec[i]=tmp3; Train_Spe[i]=tmp4
# save the model to disk
filename[i] = './Trained_Models/sgd_clf.sav'
pickle.dump(sgd_clf, open(filename[i], 'wb'))
Logistic Regression¶
lr_clf = LogisticRegression(max_iter= 50,C=50,random_state=42)
lr_clf.fit(X_train_std,y_train)
y_train_pred=cross_val_predict(lr_clf,X_train_std,y_train, cv=3)
y_train_proba_lr=cross_val_predict(lr_clf,X_train_std,y_train, cv=3, method='predict_proba')
font = {'size' : 6}
plt.rc('font', **font)
fig = plt.subplots(figsize=(5, 5), dpi= 250, facecolor='w', edgecolor='k')
ax1=plt.subplot(1,2,1)
i=2
tmp1,tmp2,tmp3,tmp4=prfrmnce_plot.Conf_Matrix(y_train,y_train_pred.reshape(-1,1),axt=ax1,
t_fontsize=6,x_fontsize=5,y_fontsize=5,title='Logistic Regression')
Train_Accu[i]=tmp1; Train_Pre[i]=tmp2; Train_Rec[i]=tmp3; Train_Spe[i]=tmp4
# save the model to disk
filename[i] = './Trained_Models/lr_clf.sav'
pickle.dump(lr_clf, open(filename[i], 'wb'))
Support Vector Machine¶
svm_clf = LinearSVC(C=60,loss='hinge',random_state=42)
svm_clf.fit(X_train_std,y_train)
y_train_pred=cross_val_predict(svm_clf,X_train_std,y_train, cv=3)
y_train_proba_svm=y_train_pred
font = {'size' : 6}
plt.rc('font', **font)
fig = plt.subplots(figsize=(5, 5), dpi= 250, facecolor='w', edgecolor='k')
ax1=plt.subplot(1,2,1)
i=3
tmp1,tmp2,tmp3,tmp4=prfrmnce_plot.Conf_Matrix(y_train,y_train_pred.reshape(-1,1),axt=ax1,
t_fontsize=6,x_fontsize=5,y_fontsize=5,title='Support Vector Machine')
Train_Accu[i]=tmp1; Train_Pre[i]=tmp2; Train_Rec[i]=tmp3; Train_Spe[i]=tmp4
# save the model to disk
filename[i] = './Trained_Models/svm_clf.sav'
pickle.dump(svm_clf, open(filename[i], 'wb'))
Decision Trees¶
tree_clf = DecisionTreeClassifier(max_depth= 10, min_samples_leaf= 15, min_samples_split=2, random_state=42)
tree_clf.fit(X_train_std,y_train)
y_train_pred=cross_val_predict(tree_clf,X_train_std,y_train, cv=3)
y_train_proba_dt=cross_val_predict(tree_clf,X_train_std,y_train, cv=3, method='predict_proba')
font = {'size' : 6}
plt.rc('font', **font)
fig = plt.subplots(figsize=(5, 5), dpi= 250, facecolor='w', edgecolor='k')
ax1=plt.subplot(1,2,1)
i=4
tmp1,tmp2,tmp3,tmp4=prfrmnce_plot.Conf_Matrix(y_train,y_train_pred.reshape(-1,1),axt=ax1,
t_fontsize=6,x_fontsize=5,y_fontsize=5,title='Decision Trees')
Train_Accu[i]=tmp1; Train_Pre[i]=tmp2; Train_Rec[i]=tmp3; Train_Spe[i]=tmp4
# save the model to disk
filename[i] = './Trained_Models/tree_clf.sav'
pickle.dump(tree_clf, open(filename[i], 'wb'))
Flowchart of Decision Tree for Prediction¶
# Flowchart of Decision Tree for Prediction with 3 depths. Training features (X) and target (y) are shown in the figure.
np.random.seed(42)
tree_clf = tree.DecisionTreeClassifier(max_depth=3)
tree_clf.fit(X_train_std,y_train)
fig, axes = plt.subplots(nrows = 1,ncols = 1,figsize = (8,8), dpi=200)
out = tree.plot_tree(tree_clf,fontsize=5)
for o in out:
arrow = o.arrow_patch
if arrow is not None:
arrow.set_edgecolor('red')
arrow.set_linewidth(1)
txt=''
for i in range(len(features_colums)):
txt+='X'+'['+str(i)+']='+features_colums[i]+'\n'
txt+='y=value= Exited'
plt.text(0.025,0.9, 'X and y Variables', fontsize=7,bbox=dict(facecolor='white', alpha=0.0))
plt.text(0.01,0.7, txt, fontsize=5.5,bbox=dict(facecolor='white', alpha=0.2))
fig.suptitle('Decision Tree Flowchart \n for Classification with 3 Depths', fontsize=10,y=0.86)
plt.show()
Adaptive Boosting with Decision Trees¶
ada_tree = AdaBoostClassifier(n_estimators=100, algorithm= 'SAMME.R', learning_rate= 0.01, random_state=42)
ada_tree.fit(X_train_std,y_train)
y_train_pred=cross_val_predict(ada_tree,X_train_std,y_train, cv=3)
y_train_proba_ada=cross_val_predict(ada_tree,X_train_std,y_train, cv=3, method='predict_proba')
font = {'size' : 6}
plt.rc('font', **font)
fig = plt.subplots(figsize=(5, 5), dpi= 250, facecolor='w', edgecolor='k')
ax1=plt.subplot(1,2,1)
i=5
tmp1,tmp2,tmp3,tmp4=prfrmnce_plot.Conf_Matrix(y_train,y_train_pred.reshape(-1,1),axt=ax1,
t_fontsize=6,x_fontsize=5,y_fontsize=5,title='Adaptive Boosting with Decision Trees')
Train_Accu[i]=tmp1; Train_Pre[i]=tmp2; Train_Rec[i]=tmp3; Train_Spe[i]=tmp4
# save the model to disk
filename[i] = './Trained_Models/ada_tree.sav'
pickle.dump(ada_tree, open(filename[i], 'wb'))
Random Forest¶
rnd = RandomForestClassifier(n_estimators=50, max_depth= 25, min_samples_split= 20, bootstrap= True, random_state=42)
rnd.fit(X_train_std,y_train)
y_train_pred=cross_val_predict(rnd,X_train_std,y_train, cv=3)
y_train_proba_rnd=cross_val_predict(rnd,X_train_std,y_train, cv=3, method='predict_proba')
font = {'size' : 6}
plt.rc('font', **font)
fig = plt.subplots(figsize=(5, 5), dpi= 250, facecolor='w', edgecolor='k')
ax1=plt.subplot(1,2,1)
i=6
tmp1,tmp2,tmp3,tmp4=prfrmnce_plot.Conf_Matrix(y_train,y_train_pred.reshape(-1,1),axt=ax1,
t_fontsize=6,x_fontsize=5,y_fontsize=5,title='Random Forest')
Train_Accu[i]=tmp1; Train_Pre[i]=tmp2; Train_Rec[i]=tmp3; Train_Spe[i]=tmp4
# save the model to disk
filename[i] = './Trained_Models/rnd.sav'
pickle.dump(rnd, open(filename[i], 'wb'))
Random Forest Feature Importance¶
# Plot the importance of features
font = {'size' : 7}
plt.rc('font', **font)
fig, ax1 = plt.subplots(figsize=(6, 3), dpi= 180, facecolor='w', edgecolor='k')
importance=rnd.feature_importances_
_=prfrmnce_plot(importance, title=f'Random Forest Algorithm to Rank Importance of Features to Predict Churn Customers',
ylabel='Random Forest Score'
,clmns=features_colums,titlefontsize=10,
xfontsize=7, yfontsize=8).bargraph(perent=True, select=None,axt=ax1,
fontsizelable=7.,xshift=-0.15,yshift=0.01,ylim=[0,0.4],y_rot=90)
Neural Network¶
model_NN=ANN (input_dim=Smaller_Training.shape[1], activation= 'relu',
dropout_rate= False, neurons= 100 )
# Early stopping to avoid overfitting
monitor= keras.callbacks.EarlyStopping(monitor='val_loss', min_delta=1e-5,patience=5, mode='auto')
history=model_NN.fit(Smaller_Training,Smaller_Training_Target,batch_size=32,validation_data=
(Validation,Validation_Target),callbacks=[monitor],verbose=1,epochs=1000)
NN_plot(history)
Bootstraping (Neural Network)¶
Bootstrapping is run to achieve reliable number of epochs for neural network.
tf.get_logger().setLevel(logging.ERROR) # Disable tensorflow warning
pred_out_of_smpl= []
y_out_of_smpl = []
acr_out_of_smpl = []
# Apply 20 bootstraping sampling
n_splits=20
boot = StratifiedShuffleSplit(n_splits=n_splits,test_size=0.2, random_state=42)
num = 0
ES_epoches=[]
for train_idx, validation_idx in boot.split(X_train_std, y_train):
num+=1
x_train = X_train_std[train_idx]
t_train = y_train[train_idx]
x_validation = X_train_std[validation_idx]
t_validation = y_train[validation_idx]
y_out_of_smpl.append(t_validation)
# Call Function
model, epoch=BS_ANN(x_train=x_train,y_train=t_train,
x_Validation=x_validation,y_Validation=t_validation,neurons=100, activation= 'relu',
dropout_rate= False)
ES_epoches.append(epoch)
pred = model.predict(x_validation)
pred=[1 if i >= 0.5 else 0 for i in pred]
pred_out_of_smpl.append(pred)
acr=accuracy_score(t_validation, pred)
reca=recall_score(t_validation, pred) # == TP/(TP+FN) )
acr_out_of_smpl.append(reca)
# Record this
print('Sample #'+str(num)+', Mean Recall='+str(np.round(np.mean(acr_out_of_smpl),4))
+', S.D. Recall='+str(np.round(np.sqrt(np.var(acr_out_of_smpl)),4))
+', Epoch='+str(epoch)+', Mean Epoch='+str(int(np.mean(ES_epoches))))
# Call Function with fined-tune numebr of neurons
model_FNN=ANN (input_dim=X_train_std.shape[1], activation= 'relu',
dropout_rate= False, neurons= 100 )
# Early stopping to avoid overfitting
history=model_FNN.fit(X_train_std, y_train,batch_size=32,verbose=1,epochs=11)
font = {'size' : 6}
plt.rc('font', **font)
fig = plt.subplots(figsize=(5, 5), dpi= 250, facecolor='w', edgecolor='k')
ax1=plt.subplot(1,2,1)
i=7
pred = model_FNN.predict(X_train_std)
y_train_proba_ai=pred
y_train_pred=np.array([1 if i >= 0.5 else 0 for i in pred])
tmp1,tmp2,tmp3,tmp4=prfrmnce_plot.Conf_Matrix(y_train,y_train_pred.reshape(-1,1),axt=ax1,
t_fontsize=6,x_fontsize=5,y_fontsize=5,title='Deep Neural Network')
Train_Accu[i]=tmp1; Train_Pre[i]=tmp2; Train_Rec[i]=tmp3; Train_Spe[i]=tmp4
# save the model to disk
filename[i] = './Trained_Models/'
model_FNN.save(os.path.join(filename[i],"NN_model.h5"))
ROC Chart for Training set¶
The receiver operating characteristic (ROC) curve is another common tool used with binary classifiers. It is very similar to the precision/recall curve, but instead of plotting precision versus recall, the ROC curve plots the true positive rate (another name for recall) against the false positive rate. The FPR is the ratio of negative instances that are incorrectly classified as positive. It is equal to one minus the true negative rate, which is the ratio of negative instances that are correctly classified as negative. The TNR is also called specificity. Hence the ROC curve plots sensitivity (recall) versus 1 – specificity.
For more information and details about ROC, see ROC)
Thus every point on the ROC curve represents a chosen cut-off even though you cannot see this cut-off. What you can see is the true positive fraction and the false positive fraction that you will get when you choose this cut-off.
font = {'size' : 12}
plt.rc('font', **font)
fig,ax = plt.subplots(figsize=(6.5,6), dpi= 120, facecolor='w', edgecolor='k')
prediction_prob=[y_train_proba_dc, y_train_proba_sgd,y_train_proba_lr,y_train_proba_dt,
y_train_proba_ada,y_train_proba_rnd,y_train_proba_ai]
predictor_name=['Dummy Classifier','Stochastic Gradient Descent','Logistic Regression','Decision Trees',
'Adaptive Gradient Boosting','Random Forest','Neural Network']
prfrmnce_plot.AUC(prediction_prob,np.array(y_train), n_algorithm=len(predictor_name), label=predictor_name
,title='Receiver Operating Characteristic (ROC)')
The best model is neural network with AUC=0.91 followed by Random Forest (AUC=0.85). Lets compare accuracy, sensitivity, specificity and precision of the classifiers.
Performance of the Models on Training Set¶
font = {'size' :9 }
plt.rc('font', **font)
ax2 = ax1.twinx()
fig, ax1 = plt.subplots(figsize=(10, 3.7), dpi= 120, facecolor='w', edgecolor='k')
ax1.plot(predictor,Train_Accu*100,'go-',linewidth=1,path_effects=[pe.Stroke(linewidth=2, foreground='k'), pe.Normal()],
markersize=9,label='Accuracy',markeredgecolor='k')
ax1.plot(predictor,Train_Pre*100,'bs-',linewidth=1,path_effects=[pe.Stroke(linewidth=2, foreground='k'), pe.Normal()],
markersize=8.5,label='Precision',markeredgecolor='k')
ax1.plot(predictor,Train_Rec*100,'y*-',linewidth=2,path_effects=[pe.Stroke(linewidth=2, foreground='k'), pe.Normal()],
markersize=12,label='Sensitivity',markeredgecolor='k')
ax1.plot(predictor,Train_Spe*100,'rp-',linewidth=1,path_effects=[pe.Stroke(linewidth=2, foreground='k'), pe.Normal()],
markersize=10,label='Specificity',markeredgecolor='k')
ax1.set_xticks(np.arange(len(predictor)))
ax1.set_xticklabels(predictor,y=0.03, rotation=19)
ax1.xaxis.grid(color='k', linestyle='--', linewidth=0.8)
ax1.yaxis.grid(color='k', linestyle='--', linewidth=0.2)
plt.ylabel('Percentage of Performance',fontsize=10)
plt.title('Performance of the Models for Training Set',fontsize=14)
legend=plt.legend(ncol=2,loc=4,fontsize='11',framealpha =0.8)
legend.get_frame().set_edgecolor("black")
ax1.yaxis.set_major_formatter(mtick.PercentFormatter())
plt.yticks([0,10,20,30,40,50,60,70,80,90,100],y=0, fontsize=9)
ax1.yaxis.set_ticks_position('both')
#plt.ylim(0.55,0.75)
plt.show()
Sensitivity is very low for all classifiers that lead to very high false negatives. This is problematic for customer churn since we want to minimize false negatives prediction. We can change the threshold to decrease precision that leads to increase sensitivity. See the Figure below for the plot of precision and sensitivity for each threshold for Neural Network. By decreasing the threshold from 0.5 to 0.29, sensitivity will increase.
font = {'size' : 10}
plt.rc('font', **font)
fig = plt.subplots(figsize=(8,4), dpi= 120, facecolor='w', edgecolor='k')
pred=y_train_proba_ai
precisions, sensitivity, thresholds = precision_recall_curve(y_train, pred)
threshold_ = 0.25
plot_precision_recall_vs_threshold(precisions, sensitivity, thresholds,x=threshold_)
plt.show()
Now calculate the sensitivity and precision again with threshold 0.25. Sensitivity increases to 0.72 but precision decreases to 0.65. This threshold will apply for test set and future data.
font = {'size' : 6}
plt.rc('font', **font)
fig = plt.subplots(figsize=(5, 5), dpi= 250, facecolor='w', edgecolor='k')
ax1=plt.subplot(1,2,1)
y_p=np.array([1 if i >= threshold_ else 0 for i in pred])
_,_,_,_=prfrmnce_plot.Conf_Matrix(y_train,y_p.reshape(-1,1),axt=ax1,
t_fontsize=6,x_fontsize=5,y_fontsize=5,title=f'Deep Neural Network \n with threshold {threshold_}')
Test Set¶
Process the test data using the same approach and statistics from training set.
# Data Processing
# Convert Geography to one-hot-encoding
Geog_1hot=pd.get_dummies(test_set_strat['Geography'],prefix='Geography')
# Convert gender to 0 and 1
ordinal_encoder = OrdinalEncoder()
test_set_strat['Gender'] = ordinal_encoder.fit_transform(test_set_strat[['Gender']])
# Remove 'Geography'
test_set_strat=test_set_strat.drop(['Geography'],axis=1,inplace=False)
test_set_strat=pd.concat([Geog_1hot,test_set_strat], axis=1) # Concatenate rows
# Standardize data
X_test = test_set_strat.drop("Exited", axis=1)
y_test = test_set_strat["Exited"].values
#
clmn=['Geography_France','Geography_Germany','Geography_Spain',
'Gender','NumOfProducts','HasCrCard','IsActiveMember']
X_test_for_std = X_test.drop(clmn, axis=1)
X_test_not_std = X_test[clmn]
features_colums=list(X_test_for_std.columns)+list(X_test_not_std.columns)
#
fname = './Trained_Models/scaler.sav'
scaler_model = pickle.load(open(fname, 'rb'))
#
df_test_std=scaler_model.transform(X_test_for_std)
X_test_std=np.concatenate((df_test_std,X_test_not_std), axis=1)
Prediction on Never Seen before Data¶
Load the trained Neural Network model and apply for prediction of test set.
Now apply threshold that we applied for training set. The Figure below shows the calculated metrics for test sets.
filename = './Trained_Models'
loaded_model = keras.models.load_model(os.path.join(filename,"NN_model.h5"))
pred=loaded_model.predict(X_test_std)
font = {'size' : 6}
plt.rc('font', **font)
fig = plt.subplots(figsize=(5, 5), dpi= 250, facecolor='w', edgecolor='k')
ax1=plt.subplot(1,2,1)
y_p=np.array([1 if i >= threshold_ else 0 for i in pred])
_,_,_,_=prfrmnce_plot.Conf_Matrix(y_test,y_p.reshape(-1,1),axt=ax1,
t_fontsize=6,x_fontsize=5,y_fontsize=5,title=f'Deep Neural Network on Test set')
The sensitivity and precision have been reduced for test set because of the model has not seen the data during training. The performance can be enhanced by increasing more training data
Train Final Model with all Data¶
The final step is training the best model (Neural Network) with entire data to take advantage of all data data to train a better model. The same hyper parameters should be applied.
# Data Processing
# Read data 'Churn_Modelling.csv'
df = pd.read_csv('./Data/Churn_Modelling.csv')
# Remove 'RowNumber','CustomerId','Surname' features that are un
df=df.drop(['RowNumber','CustomerId','Surname'],axis=1,inplace=False)
# Shuffle the data
np.random.seed(32)
df=df.reindex(np.random.permutation(df.index))
df.reset_index(inplace=True, drop=True) # Reset index
# Convert Geography to one-hot-encoding
Geog_1hot=pd.get_dummies(df['Geography'],prefix='Geography')
# Convert gender to 0 and 1
ordinal_encoder = OrdinalEncoder()
df['Gender'] = ordinal_encoder.fit_transform(df[['Gender']])
# Remove 'Geography'
df_set_strat=df.drop(['Geography'],axis=1,inplace=False)
df_set_strat=pd.concat([Geog_1hot,df_set_strat], axis=1) # Concatenate rows
# Standardize data
X_df = df_set_strat.drop("Exited", axis=1)
y_df = df_set_strat["Exited"].values
#
clmn=['Geography_France','Geography_Germany','Geography_Spain',
'Gender','NumOfProducts','HasCrCard','IsActiveMember']
X_for_std = X_df.drop(clmn, axis=1)
X_not_std = X_df[clmn]
features_colums=list(X_for_std.columns)+list(clmn)
#
scaler = StandardScaler()
scaler.fit(X_for_std)
df_std=scaler.transform(X_for_std)
X_test_std=np.concatenate((X_for_std,X_not_std), axis=1)
# Retain Neural Network with entire data
Final_Model=ANN (input_dim=X_for_std.shape[1], activation= 'relu',
dropout_rate= False, neurons= 100 )
history=Final_Model.fit(X_for_std, y_df,batch_size=32,verbose=1,epochs=11)
# Save final model to disk
filename = './Trained_Models/'
model_FNN.save(os.path.join(filename,"Final_NN_model.h5"))